
Input the mean radius, length and number of turns of a coil then press 'compute' button.
If the number of turns is set to zero, only the Nagaoka coefficient will be computed.
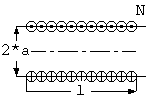
The calculation of the inductance of single-layer coil is based on formulas for a cylindrical current sheet, that is, a winding where the current flows around the axis of a cylinder of infinitesimal radial thickness on the surface of the cylinder. Except in the case of very open helical windings, the inductance of a single-layer coil is closely equal to that of a cylindrical current sheet having the same number of turns N as the coil, the same mean radius a, and length l equal to the number of turns in the coil times the distance between centers of adjucent wires.
An exact formula for the inductance of a cylindrical current sheet was first found in 1879 by Lorenz(1), who integrated the expression for the mutual inductance of two equal coaxial circular filaments twice over the length of the current sheet. Lorenz's formula is in elliptic integrals and involves both positive and negative terms.
In early days when man have no electronic computers, many forms of series aproximations and tables are developed. Among of them, Nagaoka's formula (2) is widely used till now.
L = K*u*PI*a*a*N*N/l where L = inductance of single-layer coil (H) K = Nagaoka coeeficient (0 < K <= 1) = = 4/(3*дл*sqrt(1-k^2))*((1-k^2)/k^2*K(k) - (1-2*k^2)/k^2*E(k) - k) k = 1 / sqrt(1 + (l/(2*a)^2) u = permeability (4e-7*3.1415.. for bacuum, air or nonferrous material) a = mean radius of coil (m) l = length of coil (m) N = number of turns of windings PI = 3.14159265..If K equal to 1, this foumula expresses the inductance per unit length of infinite single-layer coil. K(k) is the complete elliptic integral of first kind, E(k) is the complete elliptic integral of the second kind.
(1) Lorenz, Wied. Ann. 7, 161 (1879); B. of S.Sci. Paper 169, 117. (2) Nagaoka, Jour. Coil. Sci. Tokyo 27, 18-33, art. 6 (1909); B. of S. Sci. Paper 169, 64.