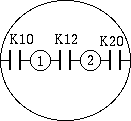
同軸ケーブル(coaxial cable)のように、 外部空間から電磁的に切り離された2 導体系の場合なら、 キャパシタンス(capacitance)も簡単で、 仕様書には内部導体と外部導体間のキャパシタンスを記述すれば済むのですが、 導体が 3 つ以上存在する多導体系(multi conductor system)だと、 そう簡単ではありません。
理由はケーブルの構造だけでなく、 回路に於けるケーブルの使い方によって、 ケーブルの実効キャパシタンスが変化するためです。
従って、ケーブルの仕様としては、 使い方に依存しない、 ケーブル固有の特性を記述しなければなりません。
この目的に最も適したパラメータが、 電気工学(electrical engineering)の部分容量(partial capacity)で、 下記のように定義されます。 (注1)
Q1 = K10*V1 + K12*(V1-V2) + .... + K1n *(V1-Vn) Q2 = K20*V2 + K21*(V2-V1) + .... + K2n *(V2-Vn) ............................................... Qn = Kn0*Vn + Kn1*(Vn-V1) + .... + Kn.n-1*(Vn-Vn-1) ここに、 Qr = r 番目の導体の電荷 (C) (0 <= r <= n) Vr = r 番目の導体と総合シールド(0 番目の導体)間の電位差 (V) Krs = r 番目の導体と s 番目の導体間の部分容量 (F) (0 <= r, s <= n)総合シールドがない場合は、地球(earth)を 0 番目の導体と考えます。
Krs は導体 r と導体 s 間の部分容量(partial capacity)あるいは 相互容量(mutual capacity)と呼ばれ、 Kr0 は自己容量(selef-capacity)あるいは 対地容量(earth capacity)とも呼ばれることもありますが、 これらは全て、 導体系の幾何学的位置関係と絶縁物の誘電特性だけで決まりますから、 回路的には全てを部分容量と考えるのが素直です。 部分容量は、多導体系の電荷と電位差の関係を 電気回路として解釈したものであることに注意してください。
例えば、2 芯シールド線の場合なら、1図のようになりますが、 Green の相反定理により、Krs = Ksr です。
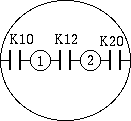
1図 - 2 芯シールド線の部分容量
部分容量の直接測定はできませんから、 複数の測定可能な部分容量の組合せから、 一次方程式を解いて求めます。
例えば、1図の場合なら、下記の手順が作れます。
K10 = (C1 - C2 + C12) / 2 K12 = (C1 + C2 - C12) / 2 K20 = (C2 - C1 + C12) / 2
導体数が多い一般の場合については、注1を見てください。
数値計算の場合も、 こういった複数の電位境界条件を作って部分容量を求めます。 計算自体は、Laplace 方程式を解くだけですから、 比較的簡単で、有限要素法を使うのが普通ですが、 外部シールドがない場合は、開領域の問題になって、 工夫が要ります。
解析的計算は、ごく限られた場合にのみ可能です。
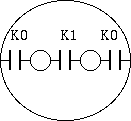
2図 - 2 芯シールド線の部分容量
部分容量がわかれば、使用時の実効キャパシタンスは、 キャパシタの直並列回路として計算するだけで、 これはケーブル利用者の仕事になります。
例えば、マイクロホンケーブルのような 2 芯のシールド線なら、 対称性により、
K0 = K10 = K20 K1 = K12と書き換えて、
平衡差動モードのキャパシタンス = K1 + K0 / 2 平衡コモンモードのキャパシタンス = K0 * 2 (2 線一括とシールド間のキャパシタンス) 1 線とシールドを接続し、残りの 1 線とで不平衡伝送を行う場合のキャパシタンス = K0 + K1です。
仕様書に表示するキャパシタンスの値は1 kHz 20℃で測定するのが普通ですが、 ポリエチレンのような無極性分子で高周波特性の良い材料では、 周波数特性がほとんどなくて、広い周波数と温度範囲で一定になります。一方、 PVCコンパウンド(ポリ塩化ビニル混和物)など、多くの絶縁材料は、 キャパシタンス、誘電損失のいずれも、周波数特性が大きく、 しかも、温度によっても、かなり変化しますから、注意が必要です。
電磁気学(electro-magnetic thory)では多導体系の電荷と電位の関係を 電位係数(coefficient of potential)か 容量係数(coefficient of capacity) で表現するのが普通ですが、 容量係数 Crs を使うと次のようになります。
Q1 = C11*V1 + C21*V2 + .... + Cn1*Vn Q2 = C12*V1 + C22*V2 + .... + Cn2*Vn .................................... Qn = C1n*V1 + C2n*V2 + .... + Cnn*Vn
これを、前記の部分容量の定義式と比較して、 部分容量と容量係数の関係を求めると、次のようになります。
Ki0 = Ci1 + Ci2 + Ci3 + .... + Cin Kij = -Cij (i != k, k != 0)容量係数を回路的に解釈するのは厄介ですが、測定は簡単で、例えば、 次のような手順が使えます。
Cij = (Ci + Cj - Ci+j) / 2
測定回数は、nCr を n 個から r 個選ぶ組合せの数として、
nC1 + nC2 = n + n!/2/(n-2)!になって、導体数が増えると、かなりの手間ですが、 多くの場合、対称性があって、通常は、もっと少ない測定回数で済みます。
静電容量係数の測定は組織的に最小手順で実行できますから、 測定実務としては、 先に静電容量係数を測定し、それを部分容量に換算するのが良いと思います。
平林 浩一, 2013-08-27