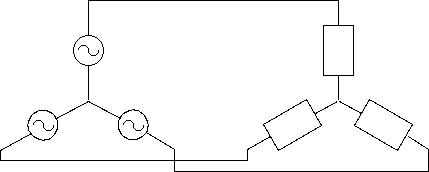
1図 Y型電源とY型負荷
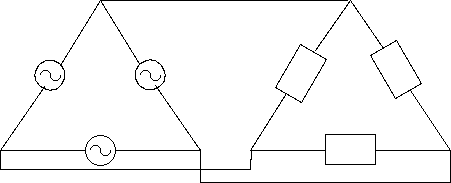
2図 Δ型電源とΔ型負荷
電気回路の理論を始めて勉強すると物理学としての電磁気学と 電気工学の電気回路理論の間のギャップにより 重要な理論(アイデア)の関連を見失うといったことがあって、 このあたりの見通しをよくする解説があってもよいのではないかと思ったのが、 これを書いた理由です。 正月休みを使って年賀状がわりに書きました。 この程度の解説で電気工学がわかるわけではありませんが、 迷路に入り込んだ方のお役にたてるかもしれません。
電気工学で扱う電磁気学の世界はMaxwell方程式で把握できるわけですが、 この方程式では電場と磁場が一体化していて、 この二つが分離できるのは極めて特殊な状況に限られます。 電気回路理論では空間の電磁場を電場だけが存在する場所と 磁場だけが存在する場所に分けるというアイデアで、 本来複雑な偏微分方程式の世界を極めて簡単な常微分方程式や 代数方程式の世界に変換してしまいます。 伝送線路のような一見電場と磁場の分離が不可能に見えるような世界までも、 Heavisideは微積分の極微の世界でこれを行うことで、 この電場と磁場の分離をやって退けます。
以下、この電場と磁場の分離という 電気回路の基盤となるアイデアを念頭に置いて、お読みください。
電気工学(注1)の基盤となる 電磁場(electromagnetic fields)の現象は、 物理学のMaxwell 方程式(注2)で記述されます。 物理的には磁場 H より磁束密度 B が本質的ですが、 電気回路(electric circuits)との関係を見るには、 H のほうがわかりやすいと思います。
| 積分型 | 微分型 | 意味 (貢献者) |
|---|---|---|
| ∮E⋅dl = (d/dt)∫B⋅dS | rot E = -(d/dt)B | 磁場の変化に起因する電場 (ファラデー) |
| ∮H⋅dl = (d/dt)∫D⋅dS + ∫i⋅dS | rot H = (d/dt)D + i | 電流と電場の変化に起因する磁場 (アンペール-マクスウェル) |
| ∫D⋅dS = ∫q⋅dV | div D = q | 電荷の実在と保存 (ガウスの法則) |
| ∫B⋅dS = 0 | div B = 0 | 磁場は電荷(電場)の動きの結果であって、磁荷は実在しない (トムソン) |
| D = ε * E, B = μ * H, J = σ * E | 空間の特性 | |
ここに、
E = 電場 (V/m) - 電界の強さと方向
D = 電束密度 (C/m^2)
= ε * E
H = 磁場 (A/m) - 磁界の強さと方向
B = 磁束密度 (Wb/m^2)
= μ * H
i = 電流密度 (A/m^2)
q = 電荷密度 (C/m^3)
μ = 透磁率 (H/m)
ε = 誘電率 (F/m)
σ = 導電率 (S/m)
∮..dl = 1周(線)積分 (contour integral)
∫..dS = 面積分 (surface integral)
∫..dV = 体積分 (volume integral)
(d/dt) = 時間微分
電気回路の動作すべてが Maxwell 方程式に基づく電磁エネルギの 移動ですから、 伝搬したエネルギの結果として回路に電流や電位差が発生するわけですが、 現実の回路の動作を直接 Maxwell 方程式で解こうとすると、 あまりに繁雑で収拾がつかなくなります。
そこで、電気工学では、 電場のエネルギだけが存在する場所をキャパシタンス (C - capacitance)素子、 磁場のエネルギだけが存在する場所をインダクダンス(L - inductance)素子、 電磁エネルギが失われる場所をレジスタンス(R - resistance)素子として認識し、 空間をこの 3 つと、 電磁エネルギを生成する電源(E - power source)に仕切ったうえで、 磁場の代わりに素子間を移動する電荷を電流として認識することで、 より取扱容易な電気回路の概念を確立しました。 電圧は電磁気学の電位差(電界の線積分)そのものです。
物理的には電磁波によって電流(電荷移動)が生まれる以上、 原因と結果が逆転(注3)していますが、 広大な空間に広がる電磁場のかわりに局所的な電気回路素子を 流れる電流と電圧を考えると、計算が極めて簡単になります。
もちろん、現実の回路部品では電場、磁場、発熱が同じ場所に混在しますから、 空間を明瞭に L, C, R に分割できないケースもありますが、 回路部品としてのコイル(coil)は磁場、キャパシタ(capacitor)は電場、 抵抗(register)は発熱がほとんどになる ように設計しますから、実用的な回路部品なら、 ごく少数の L, C, R の組み合わせで良い近似が得られますし、 本質的に電磁場が分離できない伝送線路などでは 空間を無限に小さな区間に分割し、 そこを L, C, R の直並列等価回路で表現する手法で、うまく扱うことができます。
この電気回路解釈では、 電磁場と電気回路のエネルギが次のように対応しています。 Poynting ベクトルは移動する電磁エネルギの大きさと方向を表すもので、 電磁気学では極めて重要な役割を果たします。
| エネルギの種類 | 電磁場 (局所空間) | 電気回路 (部品空間) | 対応 |
|---|---|---|---|
| 磁場 | μ * H^2 / 2 | L * I^2 / 2 | μ <-> L, H <-> I |
| 電場 | ε * E^2 / 2 | C * V^2 / 2 | ε <-> C, E <-> V |
| 回路の外に出てゆくエネルギ (ジュール熱など) | E^2 / ρ | V^2 / R | ρ <-> R |
| Poynting ベクトル (エネルギ移動) | E x H | V * I | E <-> V, H <-> I |
ここに、 V = 電気回路の電圧 (V) I = 電気回路の電流 (A) L = インダクタンス (H) C = キャパシタンス (F) R = レジスタンス(抵抗) (Ω) ρ = 抵抗率 (Ω/m)E, V と H, I の単位を比べるとわかりますが、 電圧には回路素子の長さ方向、電流には電流と直交する平面、 インダクタンスとキャパシタンスには残りの次元が取り込まれていることが、 μ (H/m) <-> L (H) と ε (F/m) <-> C (F) の対応を見るとわかります。
なお、この対応だと電圧と電流は本来 Maxwell 方程式では1周積分になるのですが、 電場と磁場を部品内部に閉じ込めた結果、部品外部の電磁場が 0 になって、 部品内部だけの積分で済むわけです。
| Maxwell 方程式 | 電気回路 |
|---|---|
| ∮E・dl | V |
| ∮H・dl | I |
この手法の良いところは、 3 次元の電磁場を回路素子という点に押し込めた結果、 回路に沿った電流という 1 次元だけが残って、 3 次元の偏微分方程式が 1 次元の常微分方程式に簡略化される ことにありますが、 Maxwell 方程式との対応を見直すと、次の電圧-電流関係が得られます。
| 電磁場 | 電気回路 | 意味 |
|---|---|---|
| ∮E⋅dL = (d/dt)∫B⋅dS | V = L * (d/dt)I | ファラデーの法則 |
| ∮H⋅dL = (d/dt)∫D⋅dS + ∫i⋅dS | I = (d/dt)Q + J = C * (d/dt)V + J |
アンペール-マクスウェルの法則 |
| ∫D⋅dS = ∫q⋅dV | V = (1 / C) * Q = (1 / C) * ∫I*dt |
ガウスの法則 |
| ∫B⋅dS = 0 | 結節点に流入する電流和 | キルヒホッフの法則 |
| 注 : ∫q⋅dV = Q 及び、 キャパシタンスでは Q = ∫I*dt, I = (d/dt)Q に注意 | ||
ここに、 J = 電流 (A) Q = 電荷 (C)
かくて、電気回路の計算は、物理空間を電気回路素子
| 電気回路素子 | 電圧-電流関係 | 意味 | ||
|---|---|---|---|---|
| L | インダクタンス (H) | V = L * (d/dt)I | 磁場エネルギ蓄積素子 | |
| C | キャパシタンス (F) | V = (1 / C) * Q = (1 / C) * ∫I*dt | 電場エネルギ蓄積素子 | |
| R | レジスタンス (Ω) | V = R * I | 電気回路から電気回路外部へのエネルギ流出素子 | |
| E, J | 電圧源 (V)、電流源 (A) | V = E, I = J | 電気回路外部から電気回路へのエネルギ供給源 | |
の電圧電流関係を使って、具体的な回路の電圧と電流を求めることに帰着しますが、 回路の電圧と電流を規定する回路方程式を組み立てるときは、 Kirchhoff の法則(注4)
なお、インダクタンスによる電圧(電位差)は、 その回路に流れる電流によるものと、他の回路に流れる電流によるものがありますから、 回路計算では、
電気回路素子のうち電気回路の世界の内部にある実体は 電界エネルギが存在するキャパシタンスと 磁界エネルギが存在するインダクタンスだけで、 レジスタンスは電気回路の世界から電気回路外に出てゆくエネルギ を現していることに注意してください。 ジュール熱のような発熱以外に、アンテナからの電磁波放射もこの一部で、 電気回路から見る限り、アンテナは電気抵抗になります。 一方、電気回路の外から電気回路にエネルギを持ち込む電気素子は 受信アンテナを含む電源です。
ここに挙げた電気回路素子は電圧と電流が比例する線形の受動素子だけですが、 電気回路ではトランジスタや FET のような非線形の能動素子もあって、 こちらは電圧と電流が比例しないため計算が極めてやっかいで、 この面倒さが 回路シミュレータSPCIEなどの開発の原動力となりました。
多くの電気回路では、L(M), C, R の回路常数(electric circuit parameters)を 定数と考えることができますが、
回路常数が時間的に変化する回転機(rotating electrical machine)の場合は、 回路常数一定の等価回路に変換できる場合が多く、 この変換が回転機理論の大きな主題になります。
回路常数が電圧(電流)依存の場合は、極端に面倒になって、 非直線問題(nonlinear circuit analysis)として扱われるのが普通です。
以下、L, C, R が定数になる線形回路(Linear Circuits) を考えます。
回路網が平面に重ならないように書ける平面回路(Flat Network)の場合は、 位相数学的関係
m = b - p + 1 ここに、 m = 編目(mesh)の数 b = 枝(branch)の数 p = 枝点(branch point)の数から、枝や枝点に比べて、編目のほうが数が少ないため、 編目を流れる 編目電流(mesh current)を変数に選ぶと 連立方程式の次元が減って、 しかも、編目電流の方向を時計回り、あるいは、反時計回りに統一することで、 Kirchhoff の第一法則(電流の代数和が 0)を自動的に満足させることができます。
従って、すべての編目電流について、Kirchhoff の第二法則、すなわち、 閉回路の電圧平衡式を作ることで、 回路の電圧・電流を完全に決定することができます。
この電圧平衡式は、電流と、その微分、積分のいずれかですから、 電流の代わりに電荷を変数に取れば、 2 階の線形連立微分方程式です。 数学的には決して難しい問題ではありませんが、 編目の数が多いと、かなり面倒になって、 この面倒を避けるために、電気工学特有の手法が生まれます。
まず、2 階の線形連立微分方程式の解は微分方程式の理論から、 定常状態の解と 過渡状態式の解の和になることがわかっています。 数学的には、 2階同次微分方程式の一般解と2階非同次微分方程式の特殊解の和になります。
例えば、電流であれば、個々の編目について、
I(t) = Is(t) + It(t) ここに、 I(t) = 編目電流 (A) Is(t) = 定常状態の編目電流 (A) It(t) = 過渡状態の編目電流 (A) = I0 * exp(α*t)の形式ですが、(工学的)過渡状態は有限時間で消滅しますから、 (振動しながらにしても)全体的には指数的に減衰する関数になります。
定常状態(steady state)というのは無限の時間が経過した後の状態ですが、 実用上は、かなり短い時間で工学的に無視できる誤差範囲に収束します。 過渡状態(trangent state)は定常状態から別の定常状態に移行する途中の状態 です。
実用的に最も重要なのが定常状態ですが、 直流回路(DC - direct current)の場合は極めて簡単で、 微分項はすべて 0 になりますから、 インダクタンスとキャパシタンスが 0、 つまり、インダクタンスは 0 Ω、キャパシタンスは∞ Ωの抵抗に置き換えて、 電源と抵抗だけの回路を解けばよいだけの話しになります。
直流についで簡単なのが交流ですが、 交流というのは電圧や電流が正弦波(sine wave)の場合です。 回転とかバネのような素直な復元機構があれば、正弦波が生まれますが、 こういった機構はどこにでもあります。 さらに、線形回路であれば、 周波数が不変に保たれる(注5)ため、 正弦波の振幅と位相だけが問題で計算が簡単、 しかも、Fourier 級数(Fourier Series)や Fourier 変換(Fourier Transform)で正弦波以外の波形も 正弦波の和に変換できますから、 交流の計算ができるだけで、実に多くの問題に対処できることになります。
なお、編目電流を使う計算法は人手による計算向きですが、 コンピュータで計算するときは、 枝点(節点 - Node)電圧を求める連立方程式を作るほうが便利で、 SPICEなどの数値計算プログラムでは先に Node 電圧を求め、 その後で電流や電力を求めます。
工学的に重要なのは、交流回路(AC circuit- alternating current circuit)で すが、その理由は前記の数学的性格に加えて 誘導電動機(induction motor)の発明にあります。 現代の産業は誘導電動機と3相交流を抜きにして成立しません。
線形の交流回路なら、回路のどの場所でも周波数一定ですから、 周波数を考える必要がなくなって、 正弦波の振幅と位相だけが問題になりますが、 電気工学の先人たちは、 振幅と位相の 2 つを要素とした簡潔なベクトル演算が成り立つような システムを発見しました。(注6)
まず、電気回路素子の電圧電流関係が単純な微積分なので、偉大な Euler の公式
exp(j * x) = cos(x) + j * sin(x) ここに、 j = sqrt(-1)を使うと、 交流電圧 E0*cos(ω*t + θ) を 2 つの共役複素数の和で表現する ことができます。
E0 * cos(ω * t + θ)
= (E0 / 2) * exp(j * ω * t + θ) + (E0 / 2) * exp(-j * ω * t - θ)
ここに、
E0 = sqrt(2) * V0 .. ピーク電圧
V0 = 交流電圧の実効値 (正弦波の 1 周期で電圧と電流の積が電力になる値)
一方、指数関数の微積分は単なる乗除演算ですから、 面倒な実数の三角関数の計算を代数化することができます。
| (d/dt)(exp(j * ω * t + θ)) = j * ω * exp(ω * t + θ) ∫exp(j * ω * t + θ)i * dt = (1 / (j * ω)) * exp(ω * t + θ) |
つまり、実数の正弦波を複素数に変換して、 2 つの共役複素数について別々に解を求め、 最後に 2 つの解から Euler の公式で実数に戻せば、 代数計算だけで済むというアイデアです。
代数化の代償として方程式の数が 2 倍になりますが、 共役複素数の性格
Re(z) = (z + conjugate(z)) / 2 Im(z) = (z - conjugate(z)) / 2 ここに、 Re(z) = 複素数 z の実部 Im(z) = 複素数 z の虚部 conjugate(z) = (複素数)z の共役複素数から、いずれか一つの解の実部ないし虚部を取れば済むことがわかって、 例えば、
cos(ω * t + θ) <-> Re(exp(j * ω * t + θ)) sin(ω * t + θ) <-> Im(exp(j * ω * t + θ))の対応で、 振幅と位相を別々に考える三角関数で表現される実数(real number)の 世界を振幅と位相の組み合わせを一体としてして 考える複素数(complex number)、 つまり2 次元ベクトル演算の世界に変換することができます。
この手法のすばらしいところは、 微分が乗算、積分が除算の代数演算に変換された結果、 連立微分方程式が連立代数方程式になってしまうことにあります。
かくて、交流の定常状態の電圧・電流計算は、 下記のような(ベクトル)インピーダンス(impedance)を考えることで、 直流回路の計算に帰着しました。
| 電気回路素子 | 電圧-電流関係 | インピーダンス | |
|---|---|---|---|
| L | インダクタンス (H) | V= j * ω * L * I | j * ω * L |
| C | キャパシタンス (F) | V = I / (j * ω * C) | 1 / (j * ω * C) |
| R | レジスタンス (Ω) | V = R * I | R |
もちろん、代数演算と言っても、複素数ですから、 直流回路に比べれば手間は増えますが、複素数の極表示を使うと 2 次元ベクトルの加減乗除には簡単な幾何学的関係があって、 少し慣れると直観的なわかりやすさがあります。
それでも、回路素子が増えるに従って、計算も面倒になりますから、 2 点から見た多数の回路素子から構成される)回路全体を 1 つの電圧源と 1 つの直列インピーダンスという 2 素子の回路に変換するテブナン等価回路(Thevenin's theorem)、 1 つの電流源と 1 つの並列インピーダンスに変換する ノートン等価回路(Norton's theorem)といった等価回路変換 の手法が開発されていて、 うまく使うと労力が大幅に減ります。
なお、電気回路のような2階常微分方程式には復元力の項がありますから、 振動現象を内包するのが最大の特徴で、 L, C という正弦波のタイミング(位相)をずらす素子を組み合わせると、 共振回路やフィルタなど、 面白くて有用な電気回路がたくさんできます。 L, C, R だけから構成される回路だけでも極めて多様性に満ちていますから、 そういった回路の一般的な性質を調べたり、 特定の周波数特性を持つ回路が合成可能かどうか、 可能なら、どういった回路になるのかといった研究も古くから行われ、 2端子回路網や4端子回路網などの理論をまとめたテキストが、 伝送回路などの名称で出版されています。
以上で交流を扱うための基盤ができましたので、次に、 電力系統で使われる3相交流を考えます。
3相交流は同じ電圧で位相が 2*π/3 (120 度) ずつ違った 3 つの電源を Y(スター型)ないしΔ(デルタ型)に組み合わせたもので、 交流発電機や誘導電動機の構造としても自然で、 しかも、変圧器により電圧の変換が容易ですから、 電気産業の基幹として使われています。
3相交流の場合は 原則として 3 つの同じ負荷をこの 2 つのいずれかの構成に接続して、 消費電力を3つの電源に均等に割り当てます。

1図 Y型電源とY型負荷 |

2図 Δ型電源とΔ型負荷 |
このような対称3相回路の場合は3相のうち1相だけで電圧、 電流を計算すれば、電力や損失ならその 3 倍、 1 相分の電圧降下なら sqrt(3) 倍すれば3相分と簡単です。
しかし、地落故障とか、単相負荷が含まれるとか、 非対称3相回路の場合は計算が極めて面倒になって一工夫必要になりますが、 最も成功した手法が対称座標法(method of symmetrical coordonates) です。(注7)
これは、回路の線形性を利用して電圧と電流を
なお、3相交流回路ではY(スター)結線とΔ(デルタ)結線が混在することが多く、 計算も複雑になりますから、 Y-Δ(スター・デルタ)変換といった簡単かつ強力な手法が開発されています。
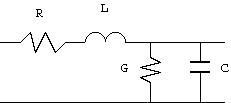
3図 分布定数線路の無限小区間
伝送線路(transmission line)など、 電場と磁場が完全に一体になっている場合は、 電場と磁場の空間を分離するのは無理みたいな気がしますが、 伝送線路を3図のような無限小区間に分割し、 その微小区間を L, R の直列回路と C, G の並列回路の和で近似してから 積分する方法で、 局所的な L, C, R, G を2次定数(secondary parameters)と呼ばれる 進行する電磁波の特性
つまり、局所的な電圧・電流を考える代わりに、 進行する電磁波の電圧・電流と速度と減衰を考えるわけで、 距離の次元が入ってきます。
このあたりの話題については、 別途解説を書きましたので、 そちらをお読みいただくか、 分布定数回路理論(distributed circuit analysis)を扱ったテキストを ご欄ください。
定常状態間の遷移、すなわち、過渡状態が問題になる場合は、 交流理論が使えず、集中定数回路の場合は 2階線形連立微分方程式をまともに解かなければなりません。 古典的な方法は、 定数係数を持つ2階非同次線形微分方程式の解を求める数学の手法を使いますが、 Laplace 変換(Laplace Transform)を使うと 微分方程式の代数化が可能で、大いに手間が省けます。 (注9)
分布定数回路の場合は常微分方程式でなく、 偏微分方程式を解くことなりますが、 この場合も Laplace 変換による解法が使えます。
また、厳密な解析解が要らなくて、回路定数が数値になっている場合は、 コンピュータ任せの Spice に代表される数値計算(numerical analysis)も使えます。
電気機械の代表が
誘導機は誘導電動機(induction motor)と 誘導発電機(induction generator)ですが、 いずれも、その機構が変圧器と似ていて、 負荷による回転数の変動(回転磁界と回転子の回転周波数差)すべり(slip)を 変圧器の二次抵抗の変化として扱うことで、 変圧器の等価回路に変換することができます。
誘導発電機は励磁電流の供給がない限り運転できませんから単体での運用は不可能で、 同期発電機との併用になりますが、 小規模の水力発電や風力発電など特殊な用途があります。
同期機のうち同期発電機は発電所の中核設備ですが、 誘導機にくらべると計算は困難です。
この他、直流機があって、優れた特性の半面、 整流子(commutator)の保守に手がかかるのが欠点で、 インバーター(inverter)等、電子制御の普及とともに利用頻度が減って、 日常いたるところで遭遇するということはなくなりました。
非線形回路の解析は線形回路に比べて極めて困難ですが、 位相幾何学的方法や摂動法(purturbation method)など、 いくつかの手法が開拓されています。 (注10)
電磁波の場合は回路理論から電磁気学に戻るのが原則ですが、 電磁波の場合も 1 次元の伝送線路が 3 次元になったと考えれば、 分布定数理論も使えるわけで、 実際、伝送線路モデル(Transmission-Line Modelling Method)と呼ばれる 手法が生まれています。
始めて電磁気学を学んだとき大きな違和感が出るのは
真空中の電磁波の速度が一定だとガリレイ相対性と矛盾するという問題は、 Maxwell が正しくてガリレイ相対性が成り立たない、つまり、 ニュートン力学が間違っているということがEinstein の特殊相対論で判明しました。 従って、ニュートン力学との矛盾は気にしなくて済みますが、 ガリレイ相対性を考慮する計算では、 単純なベクトル計算でなく相対論を考慮した光速を含む計算が必要になります。
なお、電場と磁場は独立した存在ではなくて、 本来単一の電磁場が観測者の座標系によって、 純粋な電場に見えたり、純粋な磁場に見えたり、 電場と磁場の混在に見えたりすることがあきらかになり、 特殊相対論によって電場と磁場が統一されることになりました。
電磁波が波動性と粒子性の両方を持つという問題は、 量子論、素粒子論により、 光子の数が極めて多い場合は 光子の量子力学的位相が揃う(coherent state)ことにより波動性が現れ、 少ない場合は粒子性が顕著になることがわかりました。 Maxwell 方程式の連続性は光子の数が非常に多い状況での、 近似だったわけです。
そして、この光子や電子の数が非常に多い状況こそが技術者が日常生きる世界ですから、 電気工学(electrical engineering)が使える Maxwell 方程式の世界を、 さらに簡略化した電気回路理論(electric circuit theory)の世界は 日常の強力なツールになります。 電磁場を電圧電流と解釈することで、 奇跡的に少ない労力で手早く仕事を済ませることができるわけです。
The Feynman LECTURES ON PHISICS の 16-4 Electrical technology を 見てみましょう。
When Faladay first public his remarkable discovery that a changing magnetic
flux produces an emf, he was asked (as anyone is asked when he discovers
a new fact of nature), "What is the use of it?"" All he had found was the
oddity that a tiny current was produced when he moved a wire near a magnet.
Of what possible "use" coukt that be? His answer was: "What is the use of
a new-born baby?"
Yet think of the tremendours practical applications his discovery has led
to.
..
You can see that there is an endless number of application and problems
that one take up while studying the laws of induction. The study of the
desigen of electrical machinery is a life work in itself. We cannot go
very far in that direction, but we should be aware of the fact that when
we have discovered the law of induction, we have suddenly connected our theory
to an enormous practical developement. We must, however, leave that subject
to engineers and applied scientists who are interested in working out the
details of particular applications. Phisics only supplies the base - the basic
principle that apply, no matter what. (We have not yet completed the base,
because we have yet to consider in details the properties of iron and copper.
Phisics has something to say about these as we will see a litte latter.)
Modern electrical technology began with Faraday's discoveries. The useless
baby developed into a prodigy and changed the face of the earth in ways its
proud father never imagined.
「ファラデーが磁束の変化が起電力を生ずるという注目すべき発見を報告したとき
(新しい自然法則を発見する誰もが聞かれるように)『それは何の役にたつのか』と
聞かれた。彼の発見と言えば磁石の近くで針金を動かすと微弱な電流が生まれたと
いう奇妙なできごとに過ぎない。彼は答えた。『生まれたばかりの赤ん坊は何の役
にたつのでしょう』
しかし、彼の発見から生まれた莫大な実用的用途を考えてほしい。
..
誘導法則を勉強するにつれて取り上げるべき無限の応用や問題があることに気づくだ
ろう。電気機器設計の研究それ自体が1つのライフワークになる。我々がこの問題に
深入りすることはできないが、誘導法則を発見した結果、突然我々の理論が広大な
実用上の発展に結び付いたことをよく認識すべきである。しかし、我々はこれらの
問題を個々の応用の細部に興味を持つ技術者や応用科学者に任せなければならない。
物理学は土台を供給する - 応用可能な基礎的原理、それがどんなものでもかまわない。
(我々はまだ土台を完成していない。何故なら銅や鉄の詳細な性質さえ研究中なのだ
から。これらについて物理学はある程度のことは言えるのであるが、この点については
後に述べる予定である。)
現代の電気工学はファラデーの発見で始まった。役にたたない赤ん坊が怪物に成長し、
その輝かしい父親でさえ思いもしなかった方法で地球の表面を変えてしまった。」
ファラデーの「new-born baby」の話しは、 質問の相手が学長だったり首相だったりして、 その応答も「Why sir, there is the probability that you will soon be able to tax it.」(じきに課税対象にすることができますよ)とかいろいろあります。 また、Franklin の「What is the use of an infant?」が念頭にあったのではないかと いう指摘もありますし、この質問と回答の応酬は 1816 年の Davy の化学的発見に 関するものという記述も多く、電磁誘導との関連は Feynman の思い違いかもしれま せん。
雄大かつ緻密な経済学理論を構築し、理想社会を目指した Karl Heinrich Marx の親友、 Friedrich Engels の言葉を借りれば、化学との対比で、 「電気学のなかにあるのは、古くさくて不確実な、 最終的に確証されたものでもなければ、最終的に覆されたものでもない山と積まれた 実験のがらくたであり、覚束かない足取りでの暗中模索と、 遊牧民の騎馬の群れさながらに、未知の領域をばらばらになって攻撃している たくさんの関連のない研究や実験」という混沌状態から、 Maxwell は電気と磁気のすべての法則を集めて、 古典物理学の最高峰となる電磁気学(A Treatise on Electricity & Magnetism)を まとめあげましたが、 原論文に記述された方程式は現代の記法に見られるようなすっきりした ものではなくて、凡人がその美しさを瞬時に感じとるのは困難です。
同時代の物理学者 FitzGerald は
George Francis FitzGerald, "[Review of] Heaviside's Electrical Papers" in The Scientific Writings of Late George Francis FitsGerald, ed. Joseph Larmor (Dublin, 1902)に、「Maxwell, like every other who does not live to explore the country he opened out, had not had time to investigate the most direct means of acess to the country, or the most systematic way of exoloring it. This has been reserved for Oliver Heaviside to do. Maxwell's treatise is cumbered with debris of his beilliant lines of assault, of his entrenched camps, of his battles. Oliver Heaviside has cleaned those away, has opened up a direct route, has made a road road, and has explored a considerable tarct of country.」 (Maxwell は自ら道をひらいた新世界を探求することができなかった他の短命の人々と同様に、 直接的到達手段や研究のための組織的手法を研究する時間を与えられなかった。 この仕事は Oliver Heaviside のために残されたのだ。 マックスウェルの論文は、彼の輝かしい猛攻撃の跡、 塹壕を巡らした野営の跡、戦闘の跡が累々として道を塞いでいる。 ヘビサイドはこれを一掃してまっすぐのルートを切り開き、広い道をつくり、 未開の土地を探検した)と書いているそうですが、 今私達がさしたる苦労もせずに Maxwell 方程式を理解し、応用できるのは Heaviside の洞察と努力によりその風景から意味までが変わってしまったためでした。
実態がよくわからない電気が導体中を流れる電流で伝わると考えると、 電流の謎 (電流の速さ)のような誤解が生まれ、 現実を説明できなくなります。
Kirchhoff は分光学や黒体輻射等、多方面で業績を残していますが、 マクスウェル理論以前に Lecher 線と呼ばれる往復導体に沿って電圧と電流が 光と同じ速度で伝わることを示しています。 ただ、その物理的意味を見抜けなかったため、Poynting と Heaviside に至るまで、 そのメカニズムが理解できず、 電気は水道管を流れる水のように導線の中を流れていると思われていたようです。 今でも学校で、そう教えているようですが ..
電気回路の Kirchhoff 法則は、 保存則を電気回路に適用しただけですが、 当時の電信網の発達で必要になった、 複雑な回路計算問題を解決するために考案されたものです。
線形回路で周波数不変になる理由は回路の線形性自体にありますが、 例えば、 伝送路では、何故、周波数が変わらないのかを参照してください。
交流理論の数学的基盤は複素数ですが、 電気工学に於ける複素数の有効性を明らかにしたのは Maxwell 方程式に魅せられた不遇の天才Heaviside。 その後の電気産業の発展とともに、 回転機を基盤にした3相交流が生まれ、 Heaviside と同時代のKennelyが歴史的論文
Kennelly, A. E.,- Impedance. Transaction of the AIEE. 10 (1893): 175-216で、インダクタンスを 2*π*L*sqrt(-1)、キャパシタンスを -1/(2*π*f*C*sqrt(-1)) の抵抗とみなせる場合は、代数化が可能になることを示したのですが、 それとは別に学生社会主義運動への参加を理由にドイツを追われた Steinmetzによって交流理論の基礎が完成し、本人をして 「電気工学の理論的問題はもはや既知の理論体系の範囲に到達し 「understood science」になったと言わしめます。 なお、交流の実効値の概念は Steinmetz によります。 また、この手法は数学的には定数係数常微分方程式の微分演算子による特殊解の解法 で正弦波だけ考えればよいという好運なケースになります。 今から交流理論を学ぶ場合は、 数学の演算子法を先にするほうが良いと思いますが、 教材はなかなか変わらないようです。
回路が線形であればですが、 3相それぞれの電圧、電流の大きさが違うとき、 非対称すなわち大きさの違う3相電圧を Va, Vb, Vc として、 下記のように対称成分の和に分解します。
Va0 = Va + Vb + Vc Va1 = Va + a * Vb + a^2 * Vc Va2 = Va + a^2 * Vb + a * Vc a = exp(j * 2 * π / 3) .. 1/3 周期位相を遅らせるベクトル ここに、 Va0 = 電圧の零相成分 (zero phase sequence component of voltage) Va1 = 電圧の正相成分 (positive phase sequence component of voltage) Va2 = 電圧の逆相成分 (negative phase sequence component of voltage) 1 + a + a^2 = 0, a^3 = 1 に注意[Va0, Va0, Va0] は回転しない同相(単相)電圧、 [Va1, a*Va1, a^2*Va1] は反時計方向、 [Va2, a*Va2, a^2*Va2] はそれぞれ時計方向に回転する電圧ですが、 いずれも対称3相電圧になっています。
電流の場合も上記の V を I に変えるだけで、同じように変換することができますから、 この Va0, Va1, Va2, Ia0, Ia1, Ia2 という個々の成分について 対称3相回路の計算を行い、下記の変換で元に戻します。
Va = Va0 + Va1 + Va2 Vb = Va0 + a^2 * Va1 + a * Va2 Vc = Va0 + a * Va1 + a^2 * Va2電流についても V を I に変えただけで元に戻す変換式が得られます。
下記の歴史的原論文は google で検索すれば見られます。
Charles LeGeyt Fortescue,- Method of Symmetrical Co-Ordinates Applied to the Solution of Polyphase Networks AIEE Transactions, vol. 37, part II, pages 1027-1140 (1918).
有線通信の歴史は古く、1838 年の大西部鉄道の鉄道通信として電信線の敷設が 始まっています。海底通信ケーブルも 1845 年の英海峡海底電信会社以来、 度重なる失敗を克服しつつ、1851年には公共通信を開始、1856 年には大西洋 電信会社の挑戦が始まりますが、度重なる失敗にもめげず、1866 年にようやく成功 しました。この最終段階では William Thomson が大きな役割を果たしていて、 海底ケーブルを同軸モデルで近似して、導体抵抗とキャパシタンスだけの分布定数回路 として伝送波形の歪みを計算しています。Thomson のモデルは
(d/dx)^2(I) = R * C * (d/dt)(I) ここに、 x = ケーブル端からの距離 (m) I = 電流 (A) R = 伝送線路の導体抵抗 (F/m) C = 伝送線路のキャパシタンス (F/m)という偏微分方程式ですから熱伝導方程式そのもので、 既に Fourier が扱った問題です。 このときはまだ、電磁波伝搬の真のメカニズムが理解されていません。
ケーブルの L, C の重要性に気づいて、その偏微分方程式とその解法を見出したのは 1881 年の Heaviside で、その回路モデルは
(d/dx)^2(V) = L * C * (d/dt)^(V) + (L * G + R * C) * (d/dt)(V) + R * G * Vというものですが、電信方程式(Telegram Equation)等と呼ばれていて、 歴史を調べないと Heaviside が出てきません。 この偏微分方程式で R = G = 0 の場合を考えると 単純な波動方程式になりますから、 ここで伝送線路に於ける電磁波の伝搬が明らかになります。
Heaviside はこの偏微分方程式の解析にHeaviside 演算子法 (Heaviside operational calculus)を駆使して、Heaviside の無歪条件
R / L = G / Cを得、電話回線の装荷コイル(loading coil)の有効性を主張しますが、 当時のイギリス官僚に徹底的に反発/無視されて、 アメリカの Pupine に成果を横取りされることになります。
なお、分布定数線路の代表と言える同軸ケーブル(coaxial cable)も、 Heaviside の発明で、1880 年の英国特許 1407 号だそうです。 Heaviside の意図は当時問題になっていたクロストーク(cross talk)対策に ありますが、 完全な同軸ケーブルは(電磁気学的に)独立した小宇宙になることを言明しています。
電気工学に於ける複雑な過渡状態の解法に微分方程式の代数化、 すなわち演算子法(operational calculus)を発明したのは Heaviside です。 今ではHeaviside 関数(Heaviside function)とか 単位関数(unit function)と呼ばれる不連続関数を足場に、 漸近展開、演算子の無限級数、常微分方程式の時間演算子の偏微分方程式への持ち込み といった、当時の常識を越えた発想で問題を解いて見せたため、 当時の主流である Cambridge 学派の反発を生みます。 微分方程式のテキストで知られている H.T.H.Piaggio は、
Heaviside's method seemd a kind mathematical blasphemy, a willful sinning against light. Yet Heaviside's result were always correct! Could a tree be really corrupt if it always brought forth good fruit?
と書いたそうですが、当時の Cambridge 学派の批判に対して Heaviside は「Shall I refuse my dinner because I do not fully understatnd the process of digestion?」 (消化のメカニズムがわからないから食事はしないというわけ?)と応じます。 今なら複素関数論や Laplace 変換の後知恵で歴史の1駒になりましたが、 当時はまだ複素数も一般的でない時代で、その真の数学的根拠の解明と展開は Bromwich, Carson, Levy, Van der Pol, Doetsch などに引き継がれてゆき、 今ではLaplace 演算子法(operational method of Laplace Tramsform)として て教わるのが一般的になりました。
非線形問題については Euler, Lagrange, Poisson, Helmholtz, Rayleigh などの偉人が古くから取り組んで いますが、 電気工学の歴史的な問題としては、インダクタ(inductor, reactor, coil)の鉄芯の 飽和現象によるインダクタンスの電流依存性から 生まれる鉄共振(Ferroresonance Phenomena)といった異常現象、 真空管の内部抵抗の電圧依存性による発振現象が知られていて、 真空管発振器の動作を表すVan der Pol 方程式などが研究されてきました。
その後、自動制御工学とか航空工学の発展とともに、 線形回路にはない跳躍現象(jamping)、高調波や分数調波の発生、 自励振動(self-induced oscillation)といった特異現象の解明を強いられる ことになります。同時に、パラメータ振動(parametric oscillation)、 同期引込現象(pullin synchronization)、超再生増幅作用(super regenerative amplification)などの実用化も進みます。
非線形問題の解法としてはLimit Cycleに着目する位相幾何学的手法と 摂動法の用途が広く、よく使われますが、それ以外にも個々の問題に対応する いろいろな手法が開拓されています。
平林浩一, 2012-01