クロストーク(crosstalk - 漏話)が最初に問題になったのは 既に過去の歴史になりつつある有線電話回線ですが、 今は LAN(Local Area Network) などの高周波デジタル伝送で考えなければならない問題の一つになりました。 ここでは、 有線電話回線を含むシールドなし平衡ケーブル(UTP - Unshielded Twistead Pair)のクロストーク問題の基礎を解説します。
相互キャパシタンス Cub と相互インダクタンス M で電気的に結合した短い線路のクロストークを考えます。 短いというのは、線路の長さが伝送される信号の波長に比べて十分短くて、 線路上で位相がほとんど変わらないという意味です。
クロストークについては、通常下記の三つを考えます。 log() は自然対数、log10() は常用対数ですから注意してください。 (注1)
NEXT (near-end crosstalk 近端漏話減衰量) = (1/2)*log(V1n/V2n) (neper)
= 20*log10(V1n/V2n) (dB)
FEXT (far-end crosstalk 遠端漏話減衰量) = (1/2)*log(V1n/V2f) (neper)
= 20*log10(V1n/V2f)
ELFEXT (equal level far-end crosstalk 測定遠端漏話減衰量) = (1/2)*log(V1f/V2f) (neper)
= 20*log10(V1f/V2f) (dB)
= FEXT - α
α = 線路全長の減衰量 (dB)
ELFEXT は FES/N (far-end signal-to-crosstalk attenuation) とも呼ばれます。
ELFEXT を考える理由は線路が長い場合、測定者単独では FEXT が測れないためです。

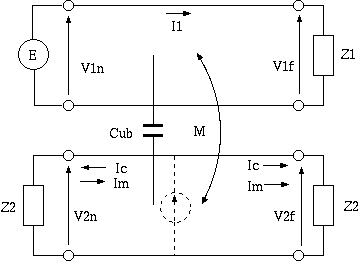
1図 短い平衡線路のクロストーク
上側の回路が誘導(ノイズ)源、下側の回路が被誘導源で、 被誘導源には、 Cub に起因する電流 Ic と M に起因する電流 Im が流れます。 Cub は被誘導回路に対して下側回路の点線で描いた定電流源として機能しますから、 被誘導回路の送端側と受端側の両方に分流して流れますが、 Im は被誘導回路の電圧源として機能しますから、 下側回路の循環電流であることに注意してください。 そのため、近端漏話は遠端漏話より小さくなります。
以下、Cub と M による被誘導回路への実際の影響を考えます。
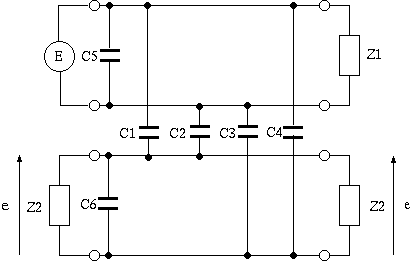
2図 キャパシタンス結合
Cub の実体は2図のキャパシタンス C1, C2, C3, C4 で、 負荷抵抗 Z2 の電圧を求めると、下記のようになります。 (注2)
e / E 〜 j*ω*Cub*Z2 / 8 (1) ここに、 Cub = (C1 + C3) - (C2 + C4) (2)
Cub はCapacitance Unbalance(容量不平衡)と呼ばれる値で、 ASTM D 4566では Cupp (Capacitance Unbalance - Pair to Pair)と表示しています。
対間クロストークでなく、1対の平衡伝送の場合は対地間容量不平衡 (Capacitance Unbalance - pair to ground) が不平衡度の指標としてつかわれます。
相互インダクタンス M による被誘導回路の電流(1図の Im)は簡単で、 下記のようになります。
Im = -j*ω*M*I1 / (2*Z2)
〜 〜-j*ω*M*E / (4*Z1*Z2) (3)
(2), (3) から Z2 の両端に現れる電圧 e1, e2 は
e1 〜 j*ω*E*(Cub*Z2/8 - M/(4*Z1*Z2)) (4) e2 〜 j*ω*E*(Cub*Z2/8 + M/(4*Z1*Z2)) (5)
FEXT より NEXT が小さいこと、 回路のインピーダンス Z1, Z2 が小さいとき M の影響が大きくて、 Z1, Z2 が大きいと Cub の影響が大きいこと、また、回路の平衡度が良くて、 Cub が小さいとキャパシタンス結合によるクロストークが小さいことがわかります。 平衡ケーブルの品質には Cub が大きな役割を果たします。
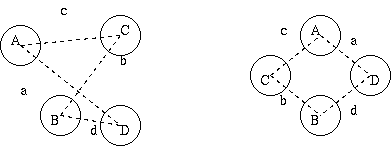
3図 2対の静電・電磁結合
Cub と M の概略値を得るために、 誘導回路の導体を A-B、被誘導回路の導体を C-D として、 2図の簡単な2対間の静電・電磁結合を考えてみると、 下記のようになります。
Cub = 72e-15*C1*C2/εs*log(a*b/(c*d)) (F/m) (6) M = 0.2e-6*μs*log(a*b/(c*d)) (H/m) (7) ここに、 C1 = 誘導回路の導体間キャパシタンス (F/m) C2 = 被誘導回路の導体間キャパシタンス (F/m) εs = 空間の比誘電率 (F/m) μs = 空間の比透磁率 (H/m)
a*b=c*d なら Cub, M のいずれも 0 になりますが、 これが電話線のQuad(カッド)構造のPhontom circuit(重信回線) と呼ばれる敷線コスト低減策として利用されます。
一般の対撚ケーブルで M がどの程度になるかは、 Nathalie Baranovの優れた研究があって、 下記の結果が知られています。(注3)
abs(M) = 1.9e-12*(r/a)^(3/2) / (5e-6 + sqrt(1 - (p1/p2)^2) / p1) * sqrt(L) (8) ここに、 abs(M) = 相互インダクタンスの絶対値 (H/m) r = 対撚の導体間距離 a = 対間距離 p1 = 一方の対の撚ピッチ (mm) p2 = 他の対の撚ピッチ (mm) .. ただし p1 < p2 L = 線路の長さ (m)
相対的対間距離 (a/r) が大きくなると M が小さくなるのは当然ですが、 2対の撚ピッチが等しい p1 = p2 のとき M が最大になって、 p2/p1 が大きくなるにつれて M が小さくなってゆくのは、 相互インダクタンスのキャンセリング機構が働くためです。 すなわち、長さ方向で相互インダクタンスの正負が反転し、 その正負のバランスで総合的な相互インダクタンス M が決まります。
p2/p1 を 1 から少しづつ大きくしてゆくにつれて M が減ってゆきますが、 p2/p1 を 1.1 より大きくしてもさして改善されるわけではありませんから、 通常の設計では p2/p1 = 1.1 程度にするのが普通です。 また、p1 を小さくしても M が減少することに注意してください。 ただ、この方針はコストアップになります。
p1 と p2 の比が整数倍のとき M が大きくなることはほとんど自明ですが、
n / p1 + m / p2 = 0 ここに、 n, m = -1, 1, 3, 5, ..のとき M が極大になることがわかっていて、2対の撚方向が同じであれば、 p2/p1 = 1 で M が最大となり、 M の値は長さと 1/p1 に比例、 撚方向が逆の場合は 1:1, 1:3, 1:5, 3:5, .. で M が極大となり、 M の値は長さと無関係になることがわかっています。
また、理論計算の結果だと M が長さ L の平方根に比例しますが、 現実の製品では撚ピッチ以外の要因もあって、 (L + sqrt(L)) / 2 程度に比例して増加することが多いようです。 L に比例する項は結合インピーダンスが長さ方向に一様な場合に現れますから、 この場合は製品自体に固有な個性があることになります。
(6), (7) の Cub と M のいずれも log(a*b/(c*d)) という幾何学的不規則性だけで決まりますから、 Cub と M には相関がありそうですが、 下記の経験則が知られています。
Cub = 0.32e-3*εs*abs(M)単位は Cub(F), M(H) です。
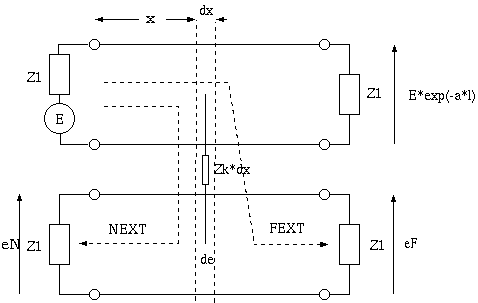
4図 2対間のクロストークの積分
長い平衡線路の場合は上記の結果を積分します。 線路の特性インピーダンスと負荷が等しくて、線路の全長を L、 ごく短い区間 dx の Cub と M による結合インピーダンスを Zk*dx とすれば、
de = Zk*E/Z1*exp(-γ*x)*dx deN = Zk*E/Z1*exp(-γ*x)*exp(-γ*x)*dx deF = Zk*E/Z1*exp(-γ*x)*exp(-γ*(L-x))*dxですから、 長さ dx に於けるクロストークによる減衰量を Ae(x) = log((2*Z1/Zk)*dx) として、 長さ方向の Zk の変動がランダムならクロストークの電力は自乗和で得られますから、
L
eN^2 = E^2*∫(exp(-2*γ*x)^2*exp(-12*Ae(x)*dx
0
L
= E^2*exp(-2*Ae(x))*∫exp(-4Aα*L)*dx
0
= E^2*exp(-2Ae(x))*(1-exp(-4α*L))/(4*α))
から、NEXT を neper 単位で書くことにして、
NEXT = log(abs(E/eN)) = Ae + 0.5*log(4*α/(1 - exp(-4*α*L))
長さが増えるに従って悪化しますが、ある程度以上になると、 一定値に収束することがわかります。
次ぎに、
L
eF^2 = E^2*∫((exp(γ1*x)*exp(-γ2*(L-x))^2*exp(-2*A(x))*dx
0
L
= E^2*exp(-2*Ae(x))*exp(-2*α*L))*∫exp(-2*(α2-α1))*dx
0
= E^2*exp(-2*A(x))*exp(-2*α2*L)*(2*(α2-α1))/(1-exp(-2*(α2-α1)L)
から、α1 = α2 = α の場合、FEXT は
FEXT = log(E/eF)
= lim(A + α2*L + 0.5*log((2*(α2-α1)/(1-exp(-2*(α2-α1)*L)))
α2->α1
= A + α*L - 0.5*log(L)
こちらは長さが増えるに従って悪化した後、
さらに長くなると再び良くなります。
同様に、ELFEXT については、 長さが長くなるにつれて、ひたすら悪化することがわかります。
前記の NEXT と FEXT は長さに対して滑らかな関数ですが、 現実の線路では始端と終端のミスマッチとか、 接続のミスマッチによる反射があって、 長さ方向のリップル(波打ち)が見られます。
以上は2対間の直接漏話を考えたわけですが、 他の対を経由した漏話まで考えると、 さらに複雑になります。
電話通信の分野では NEXT, FEXT の代わりに NXT, FXT を使います。
理論では neper 単位が素直ですが、
規格を含めて現場では dB が使われます。
理由はよくわかりませんが、
関数電卓やコンピュータが存在しない時代に
常用対数表を使ったためではないかと思います。
5.1. 注1