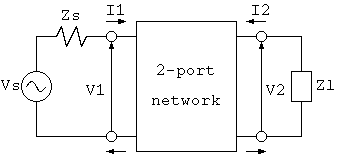
1図 2ポートネットワーク
電磁エネルギの移動は、すべて電磁波の伝搬として実現されますが、 電磁波は回路の特性インピーダンスの一様性が失われた場所で反射しますから、 回路内には無数の反射波が存在し、 電磁エネルギの分布とその時間的変化はかなり複雑です。
しかし、周波数が低く、 部品の大きさが信号波形を構成する周波数成分の波長に比べて十分小さい場合は、 反射波の影響は信号が変化する時間に比べて、 極めて短時間でなくなりますから、 定常状態としての部品内部の電圧と電流が一様になり、 その電圧、電流の比としての「インピーダンス」で 部品固有の特性を表わすことができます。
ところが、高周波の部品や回路では、 部品内部の電磁波の伝搬速度に比べて部品の大きさが無視できませんから、 部品内部に於ける電磁波の進行波と反射波の干渉の一様性が失われ、 定常状態の電圧と電流とその比が部品固有の定数ではなくなります。 つまり、 集中回路で有効な進行波と反射波の合計としての電圧・電流を基本にした 「インピーダンス」概念が使えなくなって、 進行波と反射波を分離することで、 「特性インピーダンス」として 「インピーダンス」概念を回復せざるを得ないのです。
かくて、部品の大きさを無視できない高周波回路では、

1図 2ポートネットワーク
ところで、部品内部の電圧・電流分布が一様でないということは、低周波部品の抵抗、 キャパシタ、インダクタのように2端子で考えることができず、単一部品であっても、 1図のような4端子回路として考えざるをえないということになりますが、 4端子回路では1図の電圧・電流関係、 つまり回路の特性 を表すのに、下記のようなパラメータが使われます。(注2)
[ V1 ] [ A B ] [ V2 ] [ ] = [ ] [ ] (1.1) [ I1 ] [ C D ] [ I2 ]
[ V1 ] [ Z11 Z12 ] [ I1 ] [ ] = [ ] [ ] (1.2) [ V2 ] [ Z21 Z22 ] [ I2 ]
[ I1 ] [ Y11 Y12 ] [ V1 ] [ ] = [ ] [ ] (1.3) [ I2 ] [ Y21 Y22 ] [ V2 ]
これらのパラメータはお互いに変換可能ですから、いずれか1つがわかれば、 部品の特性が把握できたことになりますが、 Zl を 0 (短絡)、ないし、無限大(開放)にすることが可能なら、 いずれのパラメータも 終端短絡か終端開放で簡単に測定できることに注意 してください。例えば、Y21 は終端短絡で V2=0 にすれば、Y21=I2/V1 となります。
しかし、トランジスタ回路の場合など、 Zl の短絡、開放という操作ができない場合も多く、 それが可能な場合でも、測定周波数が高くなると、 リード線のインダクタンスやキャパシタンスの影響が無視できなくなって、 電圧、電流の直接測定は難しくなります。
一方、方向性結合器やブリッジを利用した反射波の測定は高い周波数まで可能ですから、 入射波と反射波の合計としての電圧、電流の関係を考えるかわりに、 常に、入射波と反射波を分離して考えることにして、 入射波と反射波の関係、すなわち、 Sパラメータ (Scattering parameter)を 考えることにすれば、測定の困難さを回避しながら、 反射と遅延、減衰がつきまとう、高周波固有の問題を素直に扱うことができます。
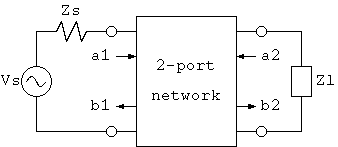
2図 2ポートネットワークとSパラメータ
1図の回路で2つの入射波(incident wave) a1, a2 と2つの 反射波(reflected wave) b1, b2 を考え(注3)、 入射波と反射波の関係を次のようにあらわします。
[ b1 ] [ S11 S12 ] [ a1 ] [ ] = [ ] [ ] (2.1) [ b2 ] [ S21 S22 ] [ a2 ]つまり
b1 = S11*a1 + S12*a2 (2.2) b2 = S21*a1 + S22*a2 (2.3)です。
この、SパラメータS11, S12, S21, S22 のすべてが実現容易な「無反射終端」で測定できることに注意してください。 例えば、Zl を2ポートネットワークの出力インピーダンスと一致させれば、 a2=0 ですから、S11=b1/a1 になります。
多くの場合、Sパラメータは「ネットワークアナライザ」を使って測定しますが、 S11 と S22 は電圧反射係数そのものですから、インピーダンス測定から計算する こともできますし、S21 と S12 は伝送特性(減衰・位相特性)そのものですから、 発振器とオシロスコープの組み合わせなどで測定することもできます。
また、Sパラメータの値は2ポートネットワークの両側の回路に 依存することに注意してください。 2ポートネットワークから見た両側の回路のインピーダンスによって、 反射波の大きさが変わりますから、 Sパラメータの値は部品固有ではなくて、 部品が置かれた回路にも依存します。
なお、上記の定義から
abs(a1)^2 = ネットワークの入力ポートに入射する電力
= 電源(インピーダンス Z0)から供給可能な電力
abs(a2)^2 = ネットワークの出力ポートに入射する電力
= 負荷から反射する電力
abs(b1)^2 = ネットワークの入力ポートから反射する電力
= 電源(インピーダンス Z0)から供給可能な電力とネットワークに
供給された電力の差
abs(b2)^2 = ネットワークの出力ポートから反射する電力
= 負荷に入射する電力
は明らかですから、S11, S12, S21, S22 の物理的意味
は
abs(S11)^2 = (ネットワークの入力端から反射される電力)/(ネットワークの入力端に入射する電力) abs(S22)^2 = (ネットワークの出力端から反射される電力)/(ネットワークの出力端に入射する電力) abs(S21)^2 = 電源と負荷のインピーダンスが Z0 のときの電力利得 abs(S12)^2 = S21 と逆方向の電力利得になります。
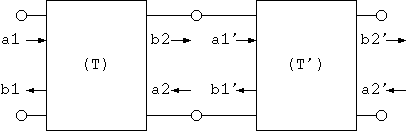
3図 従属回路
測定が簡単で物理的意味が明解なのがSパラメータの利点ですが、電子回路で頻繁に 現れる回路の従続接続に対する合成Sパラメータを求めるのは面倒で、 この場合は下記のように 定義されたTパラメータを使うのが普通です。
[ b1 ] [ T11 T12 ] [ a2 ] [ ] = [ ] [ ] (3.1) [ a1 ] [ T21 T22 ] [ b2 ]
Tパラメータを使うと3図の従属接続回路には下記の関係がありますから、
[ b1 ] [ T11 T12 ][ T11' T12' ] [ a2' ] [ ] = [ ] [ ] (3.2) [ a1 ] [ T21 T22 ][ T21' T22' ] [ b2' ]合成Tパラメータは行列の乗算で簡単に計算することができます。つまり、
[ T11 T12 ][ T11' T12' ]
T = [ ][ ] (3.2)
[ T21 T22 ][ T21' T22' ]
ここに
T = 合成Tパラメータ
になります。
SパラメータとTパラメータの関係は次のとおりです。
[ T11 T12 ] [ -(S11*S22-S12*S21)/S21 S11/S21 ] [ ] = [ ] (3.3) [ T21 T22 ] [ -S22/S21 1/S21 ] [ S11 S12 ] [ T12/T22 (T11*T22-T12*T21)/T22 ] [ ] = [ ] (3.4) [ S21 S22 ] [ 1/T22 -T21/T22 ]
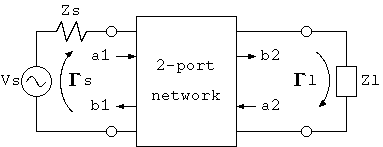
4図 2ポートネットワーク
Sパラメータによる回路計算の方法 を理解するために、4図の回路で b2 を求める ことを考えます。つまり、送受端を終端したときの伝送特性です。
まず、Sパラメータの定義から、(2.2), (2.3) が成り立ち、負荷における反射係数 を Γl とすれば a2 = Γl*b2 ですから、これを (2.3) に代入すれば
b2 = S21*a1/(1 - S22*Γl) (4.1)になります。一方、送端側の反射係数を Γs とすれば
bs = Vs*sqrt(Z0)/(Zs+Z0)として、a1 = bs + Γs*b1 ですから、これを (2.2) に代入して
a1 = bs + Γs*(S11*a1 + S12*Γs*b2) (4.2)(4.1), (4.2) から
b2 = S21*bs/((1 - Γs*S11)*(1 - S22*Γl) - Γs*Γl*S12*S21)) (4.3)で伝送特性がます。Γl と Γs はネットワークアナライザ等で直接測定すること もできますし、インピーダンス測定から次のように計算することもできます。
Γl = (Zl - Z0)/(Zl + Z0) Γs = (Zs - Z0)/(Zs + Z0) ここに Z0 = ネットワークの特性インピーダンスこのように、Sパラメータを使った計算では電圧、電流でなく、 接続点の反射係数を使います。
4図の回路を次のようなシグナルフローグラフ (signal flow graph) に変換すると計算は極めて直観的でわかりやすくなります。
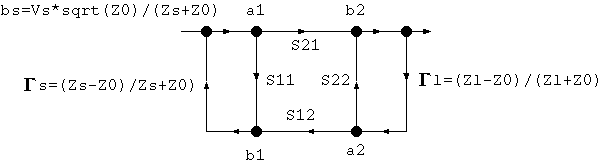
5図 4図の回路のシグナルフローグラフ
回路からシグナルフローグラフへの変換規則は次のようになっています。
接点(node) an は n 番目のポートへの入射波、接点 bn は n 番目のポートから 出て行く反射波を表します。Sパラメータは枝の両端のノードの比ですから、 枝の起点になる接点の値に枝のSパラメータの値を掛ければ枝の終点になる接点の値に なります。
フローグラフの計算方法にはいくつかの方法がありますが、よく使われるのは
トポグラフィカル(topographical)な方法と
メイソンの非接触ループ法(Mason's nontouching
loop method)と呼ばれるもので、前者は、
ネットワーク全体の応答は、波が通り抜けられることのできる全てのパスの和になる
という、量子力学のFeinman 経路積分とよく似たアプローチです。
パス(path)は入力節点から出力節点への経路
を意味します。
例えば、(4.1) 式の b2 に関するパスは、
1) a1 -> S21 2) a1 -> S21 -> Γl -> S22 3) a1 -> S21 -> Γl -> S22 -> Γl -> S22 4) a1 -> S21 -> Γl -> S22 -> Γl -> S22 -> Γl -> S22 ..と無限個の反射の総和ですから、この無限級数の和を計算して
b2 = a1*S21 + a1*S21*Γl*S22 + a1*S21*(Γl*S22)^2 + a1*S21*(Γl*S22)^3 + ..
= a1*S21/(1 - S22*Γl)
になります。同様に、(4.2) の a1 のパスは
1) bs 2) a1*S11*Γs 3) b2*Γl*S12*Γsの3つですから、
a1 = bs + a1*S11*Γs + b2*Γl*S12*Γs
= bs + Γs(a1*S11 + b2*S12*Γl)
と計算できます。
また、同じように b1 を求めると
b1 = a1*S11 + a1*S21*S12*Γl/(1 - S22*Γl)
= a1*(S11 + S21*S12*Γl/(1 - S22*Γl))
ですから、反射係数 Γl で終端したときの合成回路の S11 が
S11 + S21*S12*Γl/(1 - S22*Γl))になることがわかります。
前記の手続きを落ちなく組織的に行うには、下記の規則を使います。

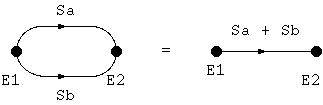
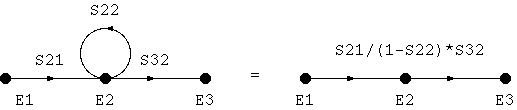
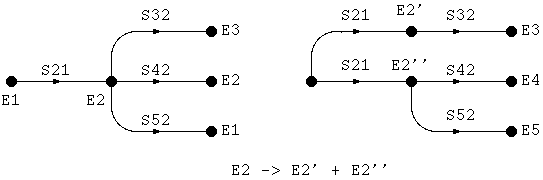
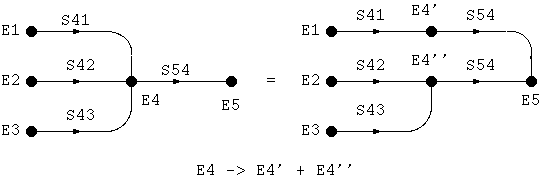
規則4はなかなか面白い使いかたができて、例えば、下記のように使うと計算は とても簡単になります。
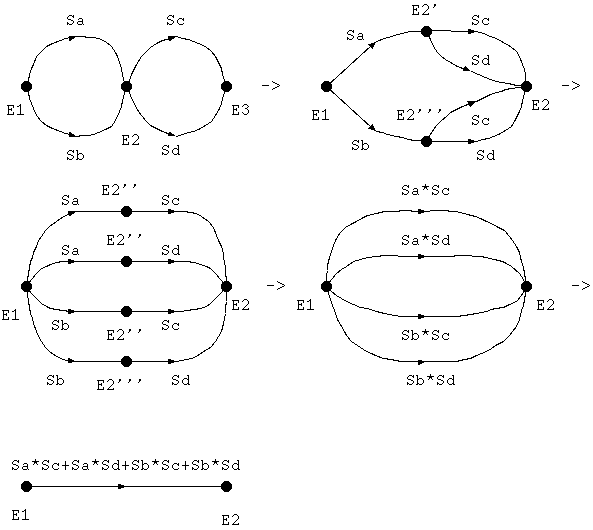
次に、先程の5図を書き直した次のフローグラフの伝達関数を求めて見ましょう。
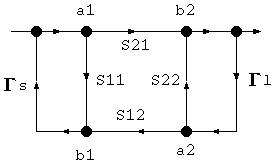
まず、b1 と a2 について規則4を適用して、
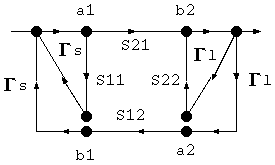
規則1を適用して、
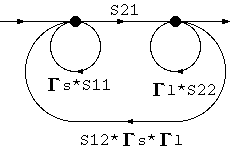
規則3と規則4を適用して、
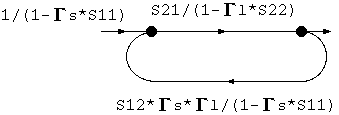
規則4を適用して、
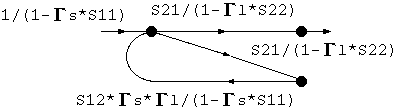
規則1を適用して、
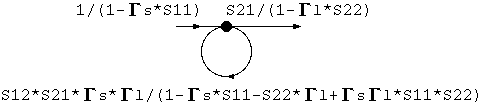
規則3を適用して、
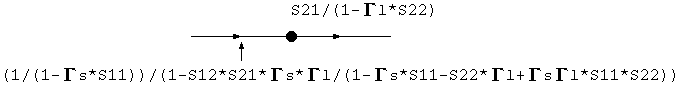
最後に規則1を適用して、
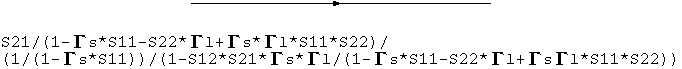
このように組織的に簡略化してゆくと間違いが減ります。
メイソンの非接触ループ法(Mason's nontouching loop method)というのは、システムの任意の2つの接点間の伝達関数を求めるための 面白い規則で、下記のようになります。
T = (1/Δ)*ΣTk*Δk
k
ここに
T = 伝達関数 = (出力数接点の値)/(入力接点の値)
Tk = k 番目の前進パスの利得
Δ = 1
- Σ(全ての独立ループの利得)
+ Σ(全ての2つの非接触ループの組み合わせについての利得の積)
- Σ(全ての3つの非接触ループの組み合わせについての利得の積)
+ ..
Δk = k 番目の前進パスに接触しない Δ の値
ここで、パス
(path)というのは連続した枝、前進パス
(forward path)は入力
接点から出力接点へのパスで同じ接点を2度以上通らないものを指します。パスの
利得
(gain)はパスに沿った全ての枝の値の積です。
ループ(loop)は出発点になった接点に戻るような
パスで、同じ接点を2度以上通らないものです。
例えば5図のフローグラフを考えると、E から b2 への前進パスは1つだけで利得 は S21 になります。E から b1 へのパスは2つあって、その利得はそれぞれ S21*Γl*S12 と S11 です。独立したループは3つで、2つの非接触ループの組み合 わせは1つだけ、3つ以上の非接触ループの組み合わせはありませんから、この ネットワークのΔの値は
Δ = 1 - (S11*Γs + S21*S12*Γl*Γs + S22*Γl) + S11*S22*Γl*Γsになり、bs から b2 への伝達関数は
b2/bs = S21/Δ
= S21/((1-S11*Γs)(1-S22*Γl)-S21*S12*Γl*Γs)
と (4.3) と同じ結果が得られます。
以下、同じように非接触ループ法を使ってよく必要になる特性を計算すると、 次のようになります。
任意の送端、受端インピーダンスに対する電力利得は
Gt = (負荷に伝送される電力)/(電源から供給可能な電力) = Pl/Pa Pl = 入射電力 - 反射電力 = abs(b2)^2*(1-abs(Γl)^1) Pa = abs(E)^2/(1-abs(Γs)^2)と (4.3) から
Gt = abs(b2/E)^2*(1-abs(Γs)^2)*(1-abs(Γs)^2)
= abs(S21)^2*(1-abs(Γs)^2)*(1-abs(Γl)2)
/abs((1-S11*Γs)(1-S22*Γl)-S21*S12Γl*Γs)^2
任意の終端インピーダンスで Zs=Z0 に於ける入力反射係数は
S11' = b1/a1
= (S11*(1-S22*Γl)+S21*S12*Γl)/(1-S22*Γl)
= S11 + S21*S12*Γl/(1 - S22*Γl)
任意の終端、送端インピーダンスに対する電圧利得は
V1 = (a1+b1)*sqrt(Z0) = Vi1+Vr1 V2 = (a2+b2)*sqrt(Z0) = Vi2+Vr2 a2 = Γl*b2 b1 = S11'*a1から
V2/V1 = b2*(1-Γl)/a1/(1+S11')
= S21*(1+Γl)/(1-S22*Γl)/(1+S11')
高周波に於ける回路特性を表現するパラメータとしては Sパラメータを使うのが普通ですが、 回路計算については、以下に述べるSパラメータとZパラメータ、Yパラメータ、 hパラメータ等の変換公式を使って、 低周波で使われる標準的な手法を利用することもできます。
特に、ZパラメータとSパラメータの関係を伝送線路理論の反射係数と比べると、 Sパラメータの意味がよくわかりますので、 ご注目ください。
以下の変換式では、Z11, Z12, Z21, Z22, Y11, Y12, Y21, Y22, h11, h12, h21, h22 のすべてが2ポートネットワークの入力(左)側のインピーダンス Z1 と 出力(右)側のインピーダンス Z2 で 規格化されていて 、 実際のパラメータ Z11', Z12', Z21', Z22', Y11', Y12', Y21', Y22', h11', h12', h21', h22' の値は次のようになることに注意してください。
Z11'=Z11*Z1, Z12'=Z12*Z2, Z21'=Z21*Z1, Z22'=Z22*Z2 Y11'=Y11/Y1, Y12'=Y12/Y2, Y21'=Y21/Y1, Y22'=Y22/Y2 h11'=h11*z1, h12'=h12, h21'=h21, h22'=h22/z2ただし、Fパラメータについては、後の説明のため、規格化しない実値にしてあります。
2図の電源側の電圧と電流を v1, i1、負荷側の電圧と電流を v2 と i2 とすれば、
[ v1 ] [ a1 ] [ b1 ] [ ] = [ ] + [ ] [ v2 ] [ a2 ] [ b2 ] [ i1 ] [ a1 ] [ b1 ] [ ] = [ ] - [ ] [ i2 ] [ a2 ] [ b2 ]の関係がありますから、これらの行列とベクトルを
[ v ] = [ a ] + [ b ] (6.1) [ i ] = [ a ] - [ b ] (6.2)と簡潔に書くことにして、Z行列が存在すれば、
[ v ] = [ z ] * [ i ] (6.3)(6.3) に (6.1) と (6.2) を代入して整理すれば、 [ 1 ] を単位行列として、
([ z ] + [ 1 ]) * [ b ] = ([ z ] - [ 1 ]) * [ a ] (6.4)
一方、(2.1) は
[ b ] = [ S ] * [ a ] (6.5)ですから、(6.4) と (6.5) を比較すれば、
[ S ] = inv([ z ] + [ 1 ]) * ( [ z ] - [ 1 ]) (6.6)が得られます。
ここで、(6.6) 式を1端子対の伝送線路に於ける反射係数の式、
γ = (Z - 1) / (Z + 1) ここに、 γ = 反射係数 Z = 規格化負荷インピーダンス (= 負荷インピーダンス / 線路の特性インピーダンス)と比べてみると、 伝送線路理論の反射係数の多次元拡張になっている ことがよくわかると思います。 これがSパラメータの意味です。
(6.6) 式の個々の成分を計算すると、下記の変換公式が得られます。
S11 = ((Z11-1)*(Z22+1)-Z12*Z21)/((Z11+1)*(Z22+1)-Z12*Z21) S12 = 2*Z12/((Z11+1)*(Z22+1)-Z12*Z21) S21 = 2*Z12/((Z11+1)*(Z22+1)-Z12*Z21) S22 = ((Z11+1)*(Z22-1)-Z12*Z21)/((Z11+1)*(Z22+1)-Z12*Z21) Z11 = (1+S11)*(1-S22)+S12*S21/((1-S11)*(1-S22)-S12*S21) Z12 = 2*S12/((1-S11)*(1-S22)-S12*S21) Z21 = 2*S21/((1-S11)*(1-S22)-S12*S21) Z22 = (1+S22)*(1-SR11+S12*S21/((1-S11)*(1-S22)-S12*S21)
以下、同様に他のパラメータとの関係を求めると、 次のようになります。
S11 = ((1-Y11)*(1+Y22)+Y12*Y21)/((1+Y11)*(1+Y22)-Y12*Y21) S12 = -2*Y12/((1+Y11)*(1+Y22)-Y12*Y21) S21 = -2*Y21/((1+Y11)*(1+Y22)-Y12*Y21) S22 = ((1+Y11)*(1-Y22)+Y12*Y21)/((1+Y11)*(1+Y22)-Y12*Y21) Y11 = ((1+S22)*(1-S11)+S12*S21/((1+S11)*(1+S22)-S12*S21) Y12 = 2-*S12/((1+S11)*(1+S22)-S12*S21) Y21 = 2-*S21/((1+S11)*(1+S22)-S12*S21) Y22 = ((1+S11)*(1-S22)+S12*S21/((1+S11)*(1+S22)-S12*S21)
S11 = (sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) - sqrt(Z1(Z2)*C - sqrt(Z1/Z2)*D) /(sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) + sqrt(Z1*Z2)*C + sqrt(Z1/Z2)*D) S21 = 2*sqrt(Z2/Z1) /(sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) + sqrt(Z1*Z2)*C + sqrt(Z1/Z2)*D) S12 = 2*sqrt(Z1/Z2) /(sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) + sqrt(Z1*Z2)*C + sqrt(Z1/Z2)*D) S22 = -sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) - sqrt(Z1(Z2)*C + sqrt(Z1/Z2)*D /(sqrt(Z2/Z1)*A + B/sqrt(Z1*Z2) + sqrt(Z1*Z2)*C + sqrt(Z1/Z2)*D) A = ((1 + S11)*(1 - S11) + S21*S12) / 2 / S21 B = ((1 + S11)*(1 + S22) - S21*S12) / 2 / S21 * Z2 C = ((1 - S11)*(1 - S22) - S21*S12) / 2 / S21 / Z1 D = ((1 - S11)*(1 + S22) + S21*S12) / 2 / S21 * Z2 / Z1
S11 = ((h11-1)*(h22+1)-h12*h21)/((h11+1)*(h22+1)-h12*h21 S12 = 2*h12/((h11+1)*(h22+1)-h12*h21 S12 = -2*h21/((h11+1)*(h22+1)-h12*h21 S22 = ((1+h11)*(1-h22)-h12*h21)/((h11+1)*(h22+1)-h12*h21 h11 = ((1+S11)*(1+S22)-S12*S21)/((1-S11)*(1+S22)+S12*S21) h12 = 2*S12/((1-S11)*(1+S22)+S12*S21) h21 = -2*S21/((1-S11)*(1+S22)+S12*S21) h22 = ((1-S11)*(1-S22)-S12*S21)/((1-S11)*(1+S22)+S12*S21)
Sパラメータの測定に最もよく使われるのは基準インピーダンス 50Ωの 「ネットワークアナライザ」(Vector Network Analyzer) ですが、 75Ω系のSパラメータがほしい等、 他の基準インピーダンスのSパラメータに変換しなければならないことがあります。
この変換は簡単で、例えば、50Ω系のSパラメータを 75 Ω系変換するなら、 上記の「SパラメータとFパラメータの関係」を」使って、 Z1 = Z2 = 50 で 50Ω系のSパラメータを 50Ω系のFパラメータに変換し、次に、 得られたFパラメータを Z1 = Z2 = 75 として 75系のSパラメータに変換するだけです。
現場向けに 75 系の「ネットワークアナライザ」も市販されていますが、 測定のためだけにわざわざ購入する必要はありません。
ケーブルの伝送特性はFパラメータで表すのが素直で、
[ A B ] [ cosh(γ*l) Z0*sinh(γ*l) ] [ ] = [ ] [ C D ] [ sinh(γ*l)/Z0 cosh(γ*l) ] ここに、 Z0 = ケーブルの特性インピーダンス (Ω) γ = ケーブルの伝搬定数 = α + j*β α = ケーブルの減衰定数 (neper/m) β = ケーブルの位相定数 (rad/m) l = ケーブルの長さ (m)ですから、これを前記の「SパラメータとFパラメータの関係」を使って Sパラメータに変換します。
例えば、Z1 = Z2 = Zs なら、下記のようになります。
S11 = S22 = 0.5*(Z0/Zs - Zs/Z0)*sinh(γ*l) / (cosh(γ*l) + 0.5*(Z0/Zs + Zs/Z0)*sinh(γ*l)) S21 = S12 = 1 / (cosh(γ*l) + 0.5*(Z0/Zs + Zs/Z0)*sinh(γ*l))
ネットワークアナライザで測定したSパラメータの値には、 ケーブルそのものの伝送特性に加えて、 ケーブル始端とケーブル終端の反射の影響が含まれていますから、 S21 や S12 はケーブルの減衰と遅延特性そのものではありませんし、 S11 や S22 もケーブルの入力インピーダンスではありません。
しかし、 ケーブルのFパラメータと「SパラメータとFパラメータの関係」を組み合わせると、 Sパラメータとケーブルの2次定数の関係がわかりますから、 ネットワークアナライザで求めたSパラメータからケーブルの2次定数を計算する ことができます。
Z0^2/Z1/Z2 = ((1+S11)*(1+S22)-S21*S12)/(1-S11)*(1-S22)-S21*S12) (sinh(γ*l))^2*Z1/Z2 = ((1+S11)*(1+S22)-S21*S12)*((1-S11)*(1-S22)-S21*S12) /(2*S21)^2ネットワークアナライザのシステムインピーダンス(通常Zs = 50)を Zs とすれば、 Z1 = Z2 = Zs になります。
しかし、実際の測定では、例えば、ケーブルの反射が小さくて S11 〜 S22 << 1 のとき
Z0 〜 (1 + S11)/(1 - S11)*sqrt(Z1*Z2) 〜 (1 + S11)/(1 - S11)*Zs S21 〜 exp(-γ*l)ですから、Z0 の測定では S11 の誤差が拡大されます。
この誤差が小さくなるのはケーブルの電気長が半波長の整数倍のときで、 この場合、ケーブルの入力インピーダンスは
Zin = (Zs/Z0 + tanh(α*l))/(1 + Zs/Z0*tanh(α*l))ですから、ケーブルが長いか周波数が高くて α*l >> 1 なら、
Z0 〜 Zinケーブル長が短いか周波数が低くて α*l << 1 なら
Z0 〜 Zin*Zsになって、反射の影響がなくなりますから、 Z0 の測定では、S11 の絶対値が極小になる周波数を選ぶといった注意が必要です。
S21 については誤差の拡大による不安定さはありませんが、 反射が増えるに従って、 ケーブル本来の減衰から離れてゆきます。
単純な部品であれば、2ポート間の電磁波の伝搬を考えれば済みますが、 ミキサー等、3ポート以上の部品も多く、 2ポートを越えるSパラメータを考えなければならないこともあります。
ケーブルに関係する問題としては、 平衡ケーブルとかクロストークのある複数の導体系といった場合ですが、 ここでは、頻繁に必要になるシールド付き平衡ケーブルの場合を考えます。 見掛け上シールドのない平衡ケーブルもありますが、 地面や筐体とのキャパシタンスやインダクタンスがありますから、 本質的に同じです。
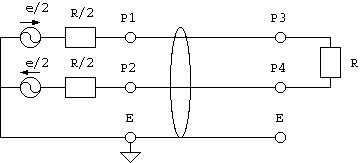
6図 平衡ケーブの原則的利用法 - Sdd (平衡-平衡) Sパラメータ
平衡ケーブルの基本的な使いかたは6図のとおりですが、 実際には送信器、受信器、ケーブルの非対称性がありますから、 (P1,P2) と (P3,P4) 間の2ポートSパラメータ Sdd を正確に求めるのは困難で、 通常は7図のように4ポートネットワークアナライザで測定します。
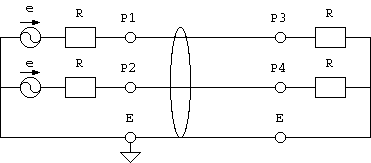
7図 4ポートネットワークアナライザによる平衡ケーブル測定
この場合、 4 つのポート P1, P2, P3, P4 に対して、反射と伝搬経路が 16 個ありますから、 下記のようなSパラメータを求めることになって、
[ S11 S12 S13 S14 ] [ S21 S22 S23 S24 ] [ S31 S32 S33 S34 ] [ S41 S42 S43 S44 ]
2ポートのネットワークアナライザで 16 通りの測定を行うのは極めて繁雑になります。
そこで、通常は、 ネットワークアナライザの入力端子に接続するポート対を自動的に切替える 4 ポートの入力を持つジグを使うことになりますが、 今度は、ジグの 4 ポートに対する校正が必要で、 反射校正を 4 回、通過(through)校正を 12 回行わなければなりません。 それでも、校正は 1 度で済みますから、測定全体としては大幅に手数が減ります。
こうして得られたSパラメータから6図の平衡伝送に置けるSパラメータ Sdd を求めるために、 7図の回路の送端(P1,P2)と受端(P3,P4)の電圧を直交する2つのベクトル、 差動(differential)成分と同相(common)成分に分解します。
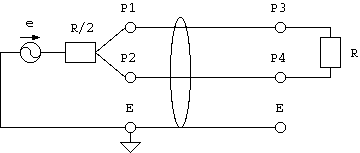
8図 Scd (同相-差動) Sパラメータ
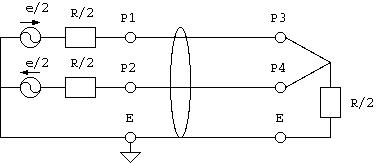
9図 Sdc (差動-同相) Sパラメータ
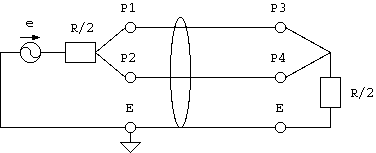
10図 Scc (同相-差動) Sパラメータ
その結果、 7図の回路を6図、8図、9図、10図の和(線形結合)に分解したことになって、 この4つの回路のSパラメータを
Sdd - 6図の「差動-差動」伝送系 (differential - differential) Scd - 8図の「同相-差動」伝送系 (common - differential) Sdc - 9図の「差動-同相」伝送系 (differential - common) Scc - 10図の「同相-同相」伝送系 (common - common)とすると、下記の関係が得られることが証明できて(注5)、 多様な伝送形態の特性が一度に得られます。
6図の回路が完全に対称で、不平衡成分がなければ、 S12 = S21, S13 = S31, S14 = S41, S23 = S32, S24 = S42, S11 = S22 = S33 = S44, S13 = S24, S14 = S42 故 Sdc, Scd がゼロになることに注意してください。 完全に独立な(干渉のない)2回路だけになります。
[ S11-S12-S21+S22 S13-S14-S23+S24 ]
Sdd * 2 = [ ]
[ S31-S32-S41+S42 S33-S34-S43+S44 ]
[ S11+S12-S21-S22 S13+S14-S23-S24 ]
Sdc * 2 = [ ]
[ S31+S32-S41-S42 S33+S34-S43-S44 ]
[ S11-S12+S21-S22 S13-S14+S23-S24 ]
Scd * 2 = [ ]
[ S31-S32+S41-S42 S33-S34+S43-S44 ]
[ S11+S12+S21+S22 S13+S14+S23+S24 ]
Scc * 2 = [ ]
[ S31+S32+S41+S42 S33+S34+S43+S44 ]
平衡ケーブルの測定法としては、 バラン(Balun - 平衡・不平衡変換器)を使って2ポートネットワークアナライザ を使う手法もありますが、 高い周波数まで使える広帯域のバランを実現するのは極めて困難ですし、 高い周波数をあきらめるにしても、 バランの校正とバランの付け替えにかなりの手間がかかりますから、 高精度・広帯域の不平衡ネットワークアナライザを使う手法は魅力的です。
「回路理論」の教科書で扱われるのが普通です。例えば、
なお、トランジスタ回路の場合は、
YパラメータとZパラメータを混ぜ合わせた
hパラメータ(h-parameter)も使われます。
回路の i 番目のポートに於ける入射波 ai と反射波 bi は
ここで、伝送線路理論でよく知られた関係
反射係数とインピーダンスの関係はスミス・チャート
(Smith Chart)の足場になっています。
線形連立方程式の解法に flow graph を使う手法は 1950 年代の前半に開発され
ましたが、連立方程式の係数行列の幾何学的関係から魔術的に解が求まる様子には、
まことに驚かされます。
中でも S.J.Mason の発明になる nonintersecting loop method は何とも不思議
ですが、これが行列式を使った線形連立方程式の解法である Cramer's rule から
証明できることを C.S.Lorens が 1956 年に証明しました。
この手法は差動モード(differential mode)と同相モード(common mode)を混合した
という意味で、
Mixed-Mode S-Parameterと呼ばれます。
下記の2章が丁寧な解説ですが、
差動モード(differential mode)とコモン(同相)モード(common mode)は直交ベクトル
ですから、7図の S11, S12, S13, S14, S21, .. S43, S44 の 16 個のパラメータから
Sdd, Sdc, Scd, Scc の 16 個のパラメータへの線形写像を考えるわけで、
線形代数の固有値問題を解くことになります。
注1- Sパラメータの発明
K.Kurokawa,- Power Waves and the Scattering Matrix
(IEEE Transactions on Microwave Theory and Techniques,
Vol.MTT-13, No.2, March, 1965)
注2- 回路のパラメータ表現
佐藤利三郎,- 伝送回路
(コロナ社) ISBN 4-339-00082-5
とかたくさんあります。
注3 - 入射波と反射波
ai = (Vi + Zi*Ii)/(2*sqrt(Re(Zi)))
bi = (Vi - Conj(Zi)*Ii)/(2*sqrt(Re(Zi)))
ここに
Vi = i 番目のポートに於ける電圧
Ii = i 番目のポートに於ける電流
Conj(z) = z の共役複素数
と任意の基準インピーダンス Zi で規格化して表しますが、通常の測定や計算では
Zi を正の実数 Z0(50 Ohm, 稀に 75 Ohm) にしますので、下記のようになります。
a1 = (V1+I1*Z0)/2/sqrt(Z0) = (ポート1への入射波の電圧)/sqrt(Z0) = Vi1/sqrt(Z0)
a2 = (V2+I2*Z0)/2/sqrt(Z0) = (ポート2への入射波の電圧)/sqrt(Z0) = Vi2/sqrt(Z0)
b1 = (V1-I1*Z0)/2/sqrt(Z0) = (ポート1からの反射波の電圧)/sqrt(Z0) = Vr1/sqrt(Z0)
b2 = (V2-I2*Z0)/2/sqrt(Z0) = (ポート2からの反射波の電圧)/sqrt(Z0) = Vr2/sqrt(Z0)
S11 = b1/a1 = (V1/I1-Z0)/(V1/I1+Z0) = (Z1-Z0)/(Z1+Z0)
Z1 = (1+S11)/(1-S11)*Z0
が得られることに注意してください。
注4 - Mason の解法
C.S.Lorens,- A PROOF OH THE NONINTERSECTING LOOP FOR THE SOLUTION OF
LENEAR EQATIONS BY FLOW GRAPHS
(Res.Lab. of Electrinics, M.I.T., Cambridge, Meas,
January, 1956 P97-102
注5 - Mixed-Mode S-Parameter
Eisenstadt, William Richard Stengel, Bob Thompson, Bruce M.,-
Microwave Differential Circuit Design Using Mixed-Mode S-Parameters
(Artech House) ISBN: 9781580539333
インタネットですぐ見られる下記の解説でも十分間に合うと思います。
W.Fan,A.C.W.Lu,L.L.Wai and B.K.Lok,-
Mixed-Mode S-Parameter Characterisation of Differential Structures