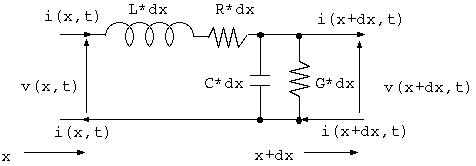
図1 一様な線路の微小部分
電磁波の伝搬路としての、 伝送線路(electrical transmission line)を扱う手法として最も一般的なのは ヘビサイドの「電信方程式」(lineman's equation)により 伝送路を「分布定数線路」 (distributed constant circuits) として扱う方法ですが、 これは電界と磁界を電圧と電流として工学的に解釈することで、 直接Maxwell方程式を扱うのと比べて計算が極めて簡単になる というのがその理由です。 以下、ケーブル伝送の理解に不可欠な、2導体系の伝送線路理論の基本を解説します。
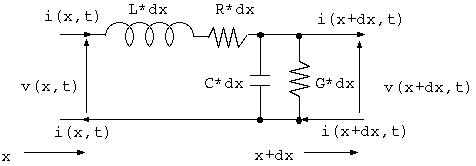
図1 一様な線路の微小部分
一様な伝送線路 の微小部分を考えます。図1の回路で往復2導体から構成される伝 送系の電圧、電流の平衡条件は
v(z+dx,t) - v(x,t) = -R*dx*i(x,t) - L*dx*(d/dt)(v(i,t)) (1.1) i(x+dx,t) - i(x,t) = -G*dx*v(x,t) - C*dx*(d/dt)(v(x,t)) (1.2) ここに v(x,t) = 距離 x、時間 t に於ける線路の電圧 (V) i(x,t) = 距離 x、時間 t に於ける線路の電流 (A) R = 線路の抵抗 (Ohm/m) L = 線路のインダクタンス (H/m) G = 線路のコンダクタンス (S/m) G = 線路のコンダクタンス (S/m) C = 線路のキャパシタンス (F/m)ですから、これらを dx で割って dx->0 の極限を考えれば、下記の偏微分方程式 が得られます。R, L, G, C は線路の静電的、電磁的特性ですが、伝送線路理論で は「1次定数 」(primary constant)と呼ばれています。(注10)
(d/dx)(v(x,t)) = -R*i(x,t) - L*(d/dt)(i(x,t)) (1.3) (d/dx)(i(x,t)) = -G*v(x,t) - C*(d/dt)(v(x,t)) (1.4)これが「電信方程式 」(lineman's equation)と呼ばれる一様な線路による伝送路の 基本的な関係になりますが、注意しなければならないのは、これは物理的な実態で なく工学的解釈であるということです。
物理的実態はあくまでもMaxwell方程式で表現される電磁界で、 これが電磁波の形で線路に沿って伝わり、 ポインティング・ベクタ(Poynting's vector)(注9) で表現されるその電磁エネルギの一部が 導体内部に入り込むことによって導体に電流が流れるわけですから、 電圧が原因になって電流が流れ、電圧と電流によってエネルギが伝送されるわけで はありません。Maxwell方程式を解いてこの偏微分方程式と比べるとわかり ますが、この方程式による表現では電磁波の電界成分の積分値を電圧、磁界成分の 積分値を電流として解釈していることになります。 (注1)
(1.3), (1.4) を x で微分して、(1.4), (1.3) を代入し、 電圧 v あるいは、電流 i だけの微分方程式を作ると、次ぎのようになります。
(d/dx)^2(v(x,t)) = L*C*(d/dt)^2(v(x,t) + (L*G + R*C)(d/dt)(v(x,t)) + R*G*v(x,t) (1.5) (d/dx)^2(i(x,t)) = L*C*(d/dt)^2(i(x,t) + (L*G + R*C)(d/dt)(i(x,t)) + R*G*i(x,t) (1.6)電圧と電流の方程式がまったく同じ形になるのは、電磁波が電界と磁界の対として 伝搬するためで、後で述べるように線路に沿った電圧と電流の比(特性インピーダン ス)は一定値になります。
以下、電圧と電流が正弦波の場合を考えますが、これは上記の方程式の扱いが簡単 で、その意味がよく理解でき、測定も簡単で、必要ならフーリエ変換と組み合わせ て任意の波形に適用できるためです。
まず、電圧と電流が正弦波の場合は交流理論 の手法で時間微分 d/dt を j*ω に置き換えて周波数ドメインに変換すれば、
(d/dx)(V) = -(R + j*ω*L)*I (1.7) (d/dx)(I) = -(G + j*ω*C)*V (1.8) および (d/dx)^2(V) - (R + j*ω*L)*(G + j*ω*C)*V = 0 (1.9) (d/dx)^2(I) - (R + j*ω*L)*(G + j*ω*C)*I = 0 (1.10) ここに j = sqrt(-1) ω = 角速度 (rad/s) V = 電圧 (V) I = 電流 (A)という定常状態の偏微分方程式が得られます。V と I は 実効値です。
(1.9), (1.10) の解は次のようになって、線路上の電圧と電流は2つの 複素数の パラメータ、特性インピーダンスと 伝搬定数で決定されることがわかります。
V(x) = V1*exp(-γ*x) + V2*exp(+γ*x) (2.1) I(x) = V1/Z0*(exp(-γ*x) - V2*exp(+γ*x)) (2.2) ここに Z0 = 特性インピーダンス(characteristic impedance) = sqrt((R + j*ω*L)/(G + j*ω*C)) (2.3) γ = 伝搬定数(propergation constant) = sqrt((R + j*ω*L)*(G + j*ω*C)) (2.4)V1*exp(-γ*x) は x 軸の正方向に伝搬する電磁波 、 V2*exp(+γ*x) は x 軸の負方向に伝搬する電磁波 を表しますが、前者を「入射波」(incident wave)、 後者を「反射波」(reflected wave)と呼ぶのが普通 です。また、
γ = α + j*β (2.5) ここに α = 減衰定数(attenuation constant) (neper/m) β = 位相定数(phase constant) (rad/s)と定義すると、αは正弦的に変化する電磁波が x 軸方向に進むときに受ける減衰 の大きさ (注 2) 、βは位相変化の大きさを表すことが確認できます。また、電磁波 の位相速度は
v = ω/β (2.6)になります。(注 3)
電磁波の波長は波動一般に成り立つ関係
β = 2*π/λ (2.7)から計算できます。
反射波の入射波に対する比を(電圧)反射係数 (reflection constant)と呼びますが、これは、
r = (Z - Z0)/(Z + Z0) (2.8) ここに Z = 任意の点から線路を見込んだインピーダンス (Ohm)になります。(注 4) ここで、「線路を見込んだ」というのはその点から先の線路の入力インピーダンス という意味で、この値を計算する方法は後述します。
例えば、特性インピーダンス Z0 の線路の終端を短絡(Z = 0)したときは r = -1 ですから線路の終端に進んだ電磁波はすべて電圧の符号が逆になって反射し、線路 の損失が小さいときは、線路上の進行波と反射波の合計は 0 になります。線路の 終端では進行波が届いたとたんに同じ大きさで符号反対の反射波が生じますから、 電圧の合計は常に 0 ですが、線路のその他の場所では進行波が到達してから反射 波が戻ってくるまでの時間だけ進行波による電圧がでます。つまり、線路の終端が どうなっているかは、反射波が戻るまでわからないことになりますが、この事実は 相対性理論と密接に関係します。電圧が 0 になるのは短絡点だけであることに注意 してください。
逆に線路の終端を開放(Z = ∞)したときは r = 1 になりますから、線路の終端に 到達した電磁波は同じ向きで同じ大きさの反射波を生じ、電圧が2倍になります。 この場合、線路の終端の電圧は最初から進行波の電圧の2倍ですが、線路の途中の 電圧は反射波が戻った時点で電圧が2倍になるわけです。
線路の終端インピーダンスが線路の特性インピーダンスと等しい(Z = Z0)ときは r = 0 (無反射)で伝送効率が最大になりますから、実用的な伝送システムでは普通 これが目標になります。
その他の終端インピーダンスでは進行波の一部が負荷に吸収され一部が反射して送 端側に戻りますから、送端側からステップ・パルスやインパルスを送り込んで、そ の反射波形を観測することで、終端インピーダンスの測定ができますし、終端イン ピーダンスがわかっていれば、特性インピーダンスや伝搬定数の測定ができること になります。また、線路に不均一な場所があれば、 そこで特性インピーダンスが変化して反射がおきますから、 線路の測定や、 品質管理にも利用できて、 この種の測定を TDR(Time Domain Reflectmetry)と呼び、多くの 専用計測機が作られています。
なお、この反射係数は「S パラメータ」の「S11」と同じ ものではありません。 伝送線路理論の反射係数は進行波に対する反射を考えていますから 周波数に無関係ですし、 「S パラメータ」は正弦波の入射と反射を考えていますから、 無数の進行波の反射波の合成結果としての反射を問題にしていて、 「S11」は周波数に依存します。
以上で、一様な線路の定常状態は特性インピーダンスと伝搬定数で簡潔に記述でき ることがわかりますが、これらを線路の「2次定数 」(secondary constatnt) と呼 び、高周波に於ける伝送線路の特性表現に使われます。
以下、2次定数の周波数特性を把握するために、2次定数と1次定数の関係を実数 表現に直すと次のようになります。
α = sqrt(0.5*(sqrt((R^2+(ω*L)^2)*(G^2+(ω*C)^2)) - (ω^2*L*C - RG)))
= R / 2 / Real(Z0) + G * Abs(Z0)^2 / 2 / Real(Z0)
β = sqrt(0.5*(sqrt((R^2+(ω*L)^2)*(G^2+(ω*C)^2)) + (ω^2*L*C - RG)))
abs(Z0) = ((R^2+(ω*L)^2)/(G^2+(ω*C)^2))^(1/4)
arg(Z0) = 0.5*(atan(ω*L/R) - atan(ω*C/G))
このままでは周波数領域のふるまいがわかりにくいのですが、いくつかの周波数範
囲に分けて近似式を求めると明解になります。
ω についてべき級数展開して、R >>ω*L, G >> ω*C の条件を使うと、
α = sqrt(R*G)*(1 + (ω*L/R - ω*C/G)^2/8) β = ω*((L/2)*sqrt(G/R) + (C/2)*sqrt(R/G)) abs(Z0) = sqrt(R/G)*(1 + (ω^2*L^2/R^2 - ω^2*C^2/G^2)) arg(Z0) = (ω/2)*(L/R - C/G))
L*G << R*C, ω*L << R, G << ω*C の条件を使うと、
α = sqrt(ω*C*R/2)*(1 - (1/2)*(ω*L/R - G/ω*C)) β = sqrt(ω*C*R/2)*(1 + (1/2)*(ω*L/R - G/ω/C)) abs(Z0) = sqrt(R/ω/C)*(1 + (ω^2*L^2/R^2 + G^2/ω^2/C^2)/4)) arg(Z0) = -(π/4 - (ω*L/R + G/ω/C))
ω*L >> R, ω*C >> G の条件を使うと、
α = (R/2)*sqrt(C/L) + (G/2)*sqrt(L/C))*(1 - (R/ω/L - G/ω/C)^2/8)
β = ω*sqrt(L*C)*(1 + (R/ω/L - G/ω/C)/8)
abs(Z0) = sqrt(L/C)*(1 + ((R/ω/2)^2 - (G/ω/C)^2))
arg(Z0) = (1/2)*(G/ω/C - R/ω/L)*(1 - (1/3)*((R/ω/L)^2
+ (R/ω/L)*(G/ω/C) + (G/ω/C)^2))
以上から、2次定数は概略次のような周波数特性を持つことがわかります。
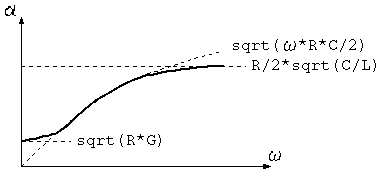
図2 減衰定数
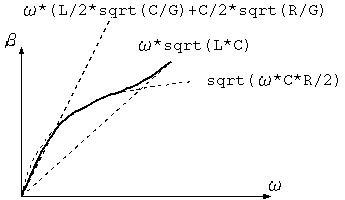
図3 位相定数
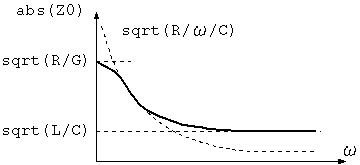
図4 特性インピーダンスの絶対値
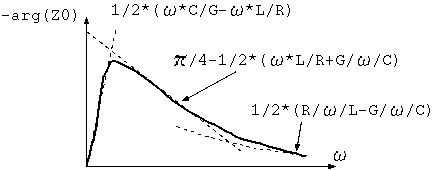
図5 特性インピーダンスの偏角
ただし、この図は1次定数(R, L, G, C)に周波数特性がないときの値で、現実のケ ーブルでは物理的に不可避な導体の渦電流 により、高周波の R は周波数の平方根 に比例して増加しますから、 減衰定数も高周波で一定になるわけでなく、周波数の 平方根に比例して増加 することに注意が必要です。位相定数も同様に周波数の平方 根に反比例してわずかに減少し、これがパルス伝送では大きな影響を与えます。
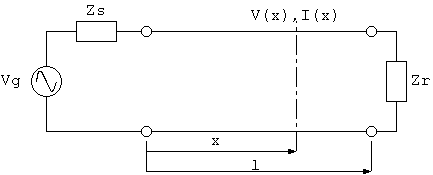
図6 伝送系 (両端を終端した線路)
線路の両端に送信器と受信器を接続したときの 送受端から見た伝送特性 は次のようになります。(注5)
Vr = cosh(γ*l)*Vs - Z0*sinh(γ*l)*Is (3.1) Ir = -(1/Z0)*sinh(γ*l)*Vs + cosh(γ*l)*Is (3.2) Vs = cosh(γ*l)*Vr + Z0*sinh(γ*l)*Ir (3.3) Is = (1/Z0)*sinh(γ*l)*Vr + cosh(γ*l)*Ir (3.4) ここに Vr = 受端の電圧 (V) Ir = 受端の電流 (A) Vs = 送端の電圧 (V) Is = 送端の電流 (A) l = 線路の長さ (m)sinh(), cosh() は複素変数の双曲線関数ですが、この関係は次のように4端子回路 の縦続行列に書き換えると意味がわかりやすくなります。
[Vs] [ A B ][Vr] [ ] = [ ][ ] [Is] [ C D ][Ir] A = cosh(γ*l) B = Z0*sinh(γ*l) C = (1/Z0)*sinh(γ*l) D = cosh(γ*l)
つまり
A*D - B*C = (cosh(γ*l))^2 - (sinh(γ*l))^2 = 1 かつ A = Dですから、可逆で対称(symmetric)な4端子回路になります。 ケーブルには方向性がなくて、どちらの端から電磁波を送り込んでも同じ特性です。
線路上の任意の場所に置ける電圧と電流 は送端と受端の反射係数を使うと簡単に表現でき て、下記のようになります。
V(x) = (Z0*Vg/(Zs+Z0))*(exp(-γ*x)*(1+rR*exp(-2*γ*(l-x))) /(1-rS*rR*exp(-2*γ*l)) (3.5) I(x) = (Vg/(Zs+Z0))*(exp(-γ*x)*(1-rR*exp(-2*γ*(l-x))) /(1-rS*rR*exp(-2*γ*l)) (3.6) ここに V(x) = 位置 x に於ける線路の電圧 (V) I(x) = 位置 x に於ける線路の電流 (A) Vg = 発信器の出力電圧 (V) rS = (Zs-Z0)/(Zs+Z0) = 送端の反射係数 rR = (Zr-Z0)/(Zr+Z0) = 受端の反射係数ここで、線路長 l がある程度長く、exp(-2*γ*l) << 1 のとき、(3.5) を exp(-2*γ*l) のべき級数に展開すると、
V(x) = (Z0*Vg/(Zs+Z0)) *(exp(-γ*l) + rR*exp(-γ*(2*l-x)) + rR*rS*exp(-γ*(2*l+x)) .. )ですから、exp(-γ*l) が送端から入射した電磁波、rR*exp(-γ*(2*l-x))、 rR*exp(-γ*(2*l-x)) はそれが一度受端で反射されて x 点に戻った電磁波、 rR*rS*exp(-γ*(2*l+x)) は受端で反射され送端の戻ってまた反射された電磁波とい うわけで、定常状態の線路は多数の反射波の合成 であることが確認できます。
ケーブルによる減衰の周波数特性を考えるために 受信器の電圧と送信器の電圧の比 を計算すると次のようになります。
Vr/Vg = (Zr/(Zs+Zr))/(cosh(γ*l)+(Z0/(Zs+Zr))(1+Zs*Zr/(Z0^2))*sinh(γ*l)
=((cosh(α*l)+a*sinh(α*l))*cos(β*l)
-j*(sinh(α*l)+a*cosh(α*l))*sin(β*l))
/((sinh(α*l)+a*cosh(α*l))^2 + (1-a^2)*(cosβ*l))^2)
ここに
a = (z0/(Zs+Zr))*(1+Zs*Zr/(Z0^2)
この x+j*y 形式を絶対値と偏角で表現すると次のようになります。
abs(Vr/Vg) = 1/((sinh(α*l)+a*cosh(α*l))^2 + (1-a^2)*(cos(β*l))^2)
arg(Vr/Vg) = (sinh(α*l)+a*cosh(α*l))*sin(β*l)
/(cosh(α*l)+a*sinh(α*l))*cos(β*l)
これを見ると、インピーダンスのマッチングが取れていて Z0 = Zs = Zr なら、
Vr/Vg = exp(-α*l - j*β*l)で、減衰と位相遅れがケーブルの長さに比例するという素直な関係になることがわ かります。
また、インピーダンスのマッチングが取れていないときは、
β*l = π/2, 3*π/2, 5*π/2, (2n-1)*π/2の周期で減衰が大きくなったり小さくなったり波うつこともわかります。つまり、 後で述べる定在波が発生します。
ケーブルを取り去って、直接受端と送端を接続してときの負荷電圧に対する ケーブル挿入時の負荷電圧を挿入比(insertion ratio) と呼びますが、挿入比が Vr/Vg の (Zs+Zr)/Zr 倍になることは、 すぐわかると思います。
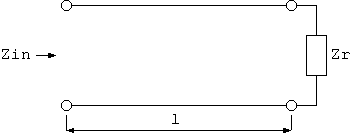
図7 終端した線路の入力インピーダンス
線路に特定の終端インピーダンスを接続したときの 入力インピーダンスは次のよう になります。(注 6)
Zin/Z0 = (Zt/Z0 + tanh(γ*l))/(1 + (Zt/Z0)*tanh(γ*l)) (4.1) ここに Zin = 線路の入力インピーダンス (Ohm) Zt = 線路の終端抵抗 (Ohm) l = 線路の長さ (m)Zt が Z0 と等しくない限り周波数に対して周期的に変化しますが、Zt = 0 の終端 短絡と Zt = ∞の終端開放線路の入力インピーダンスは下記のようになって、減衰 が少ないと非常に Q の高い周期性の共振回路になりますので、分布定数回路のイン ピーダンス整合素子として利用されることがあります。
Zsc = Z0*tanh(γ*l) = Z0*tanh((α+j*β)*l) (4.2)
= Z0*(sinh(α*l)*cosh(α*l) + j*sin(β*l)*cos(β*l))
/((sinh(α*l))^2 + (cos(β*l))^2)
Zoc = Z0/tanh(γ*l) = Z0/tanh((α+j*β)*l) (4.3)
= Z0*(sinh(α*l)*cosh(α*l) - j*sin(β*l)*cos(β*l))
/((sinh(α*l))^2 + (cos(β*l))^2)
この2つから
Z0 = sqrt(Zsc*Zoc) (4.4) tanh(γ*l) = sqrt(Zsc/Zoc) (4.5)がでますが、この関係は「オープン・ショート法 」(Open/Short method)として、 よく2次定数の測定に利用されます。
また、減衰が少なくてα<<1で、β*l=n*π (n = 0, 1, 2, ..) つまり、線路の長 さが半波長の整数倍のときは Zin = Zt、β*l=n*π/2 (n = 0, 1, 2, ..) つまり、 線路の長さが 1/4 波長の奇数倍のときは Zin = sqrt(Z0*Zt) になりますので、 よく、狭帯域のインピーダンス整合とかインピーダンス変換に利用されますし、 線路特性の測定にも使われます。
ここで注意しなければならないのは、 分布定数回路の電圧と電流の比(Z = V/I)は 線路の負荷や線路上の位置に依存しますから、 回路部品のすべての場所で電圧・電流分布が一様な「集中定数回路」の 集中定数回路の場合と違って、定数になりません。 つまり、 インピーダンス(impedance)の概念が役にたたなくなります。 しかし、電圧、電流を進行波と反射波に分解して、 進行波だけ、反射波だけについてインピーダンスを考えれば、 集中定数と同じようにインピーダンスが定数になり、 これが「特性インピーダンス」を考える理由なのです。
なお、低周波の短い線路で、α*l<<1, β*l<<1 が成り立てば、
Zsc 〜 Z0*α*l + j*ω*L*l Yoc = 1/Zoc = α*l/Z0 + j*ω*C*lとなって、線路のインダクタンス(L)とキャパシタンス(C)の測定ができますが、キャパ シタンス測定の損失のほとんどが誘電体損失でなく導体損失であることに注意してくだ さい。
前記のように、線路の入力インピーダンスは負荷インピーダンスが線路の特性イン ピーダンスと一致しないとき、 線路には進行波と反射波の両方が存在しますから、 これらの干渉により、電圧や電流の周期的変化を生じます。 その結果、線路上の電圧分布は下記のようになって、 振幅が時間に関係なく一定になりますので、 線路上に動かない波ができたように見えますから、 これを「定在波 」(standing wave)と呼んでいます。
abs(V(d)) = sqrt(sinh(α*d+p) + (cos(β*d + q))^2) r = exp(-2*(p + j*q)) r = (Zt - Z0)/(Zt + Z0) ここに abs(x) = x の絶対値 V(d) = 線路終端から d 離れた場所の進行波と反射波の合計電圧 (V) d = 線路終端からの距離 (m) α = 減衰定数 (neper/m) β = 位相定数 (rad/m) Z0 = 線路の特性インピーダンス(Ohm) r = 線路終端に於ける反射係数
この定在波の電圧の最大値と最小値の比を電圧定在波比 (Voltage Standing Wave Ratio) と呼び、線路終端の反射係数との間には次の関係があります。
VSWR = (1 + abs(rT))/(1 - abs(rT)) (5.1) ここに VSWR = abs(max(V(x))/abs(min(V(x)) rT = (Zt-Z0)/(Zt+Z0) = 受端の反射係数VSWR そのものは線路の局所的な発熱や高電圧時の絶縁破壊の評価等で必要になりますが、 「スロットライン」(slotted line)を使ったインピーダンス測定などに 利用されるすることがあって、 今でも重要な測定手段の1つです。
歴史的事情から、現場レベルでは、インピーダンスミスマッチによる反射の評価に 「リターンロス 」(return loss)を使うことがありますが、これは次のような定義 です。
return loss = 10*log10(abs(r)^2) (dB) (6.1) ここに r = 線路終端の反射係数これは何を考えているかというと、「線路の特定の点に於いて、入射波が反射して 元の方向に戻るとき、どれだけ減衰するか」ということで、100 % 反射のとき 0 で減衰なしにすべてが反射波になり、無反射のとき無限大の損失で反射波は存在し ないという認識になります。伝送より「投資(入射)に対する return (反射)を期待 する」という、少しひねくれた見方ですが、 伝送特性の裏返しになる反射特性を測定しようという場合は この考え方も自然ではあります。
リターンロスを考えているのが線路の始端で、線路に損失がある場合は、反射波が 線路の往復分だけ減衰しますから、次のようになります。
return loss = 10*log10(abs(r)^2) + 8.686*2*α*l (dB) (6.2) ここに α = 線路の減衰定数 (neper/m) l = 線路の長さ (m)
反射による伝送損失を直接表すには「反射損失 」(reflection loss)を使うの が素直で、次のような定義になります。
reflection loss = -10*log10(1 - abs(r)^2) (dB) (6.3)こちらは、伝送効率を念頭に置いた素直な概念です。
反射係数の式 (2.8) で
Z/Z0 = rn + j*xnと、線路の終端インピーダンス Z を線路の特性インピーダンス Z0 で規格化すると 反射係数は
u + j*v = (rn + j*xn - 1)/(rn + j*xn + 1)になりますから、
(u - rn/(rn + 1))^2 + v^2 = 1/(rn + 1)^2 (u - 1)^2 + (v - 1/xn)^2 = (1/xn)^2になって、rn が一定の場合も xn が一定の場合も (u,v) 点は円になります。しか も線路を見込んだインピーダンスが u^2+v^2=1 の同心円上を線路の長さに対応 する角度で移動することが証明できますので、少し慣れると線路に沿ったインピー ダンスの変化を直観的に把握しやすい図表を作ることができて、 「 スミスチャート」 (Smith Chart)(注8)と呼ばれています。
今は面倒な計算もコンピュータで簡単にできますので、使いかたの説明には触れま せんが、必要になったら実務書を見てください。高周波の伝送線路を扱う場合、 慣れていて損のない道具(graphical aid)です。コンピュータが使えない時代には、 これが高周波の最も有効な計算、設計手段でした。
定常状態の伝送線路を考える限り双曲線関数しか使いませんから、あまり面倒な計 算にはなりませんが、よく必要になる公式(関係式)をまとめておきます。双曲線関 数は指数関数の組み合わせですから、オイラーの公式により、複素領域で三角関数 と密接なつながりがあります。人類にとって長年疑問の種だった複素数(虚数)を自 信を持って使えるようになったのは、偉大なオイラーの貢献です。今まで気にして いなかった方は、方程式 cos(x)^2 = 2 の根とか、j^j, j^(-j) などを考えてみるの も楽しいと思います。
sinh(x) = (exp(x) - exp(-x))/2 cosh(x) = (exp(x) + exp(-x))/2 tanh(x) = sinh(x)/cosh(x) coth(x) = 1/tanh(x) cosh(x)^2 - sinh(x)^2 = 1 sinh(-x) = -sinh(x) cosh(-x) = cosh(x) tanh(-x) = -tanh(x) coth(-x) = -coth(x) sinh(x + y) = sinh(x)*cosh(y) + cosh(x)*sinh(y) cosh(x + y) = cosh(x)*cosh(y) + sinh(x)*sinh(y) tanh(x + y) = (tanh(x) + tanh(y)) / (1 + tanh(x) * tanh(y)) coth(x + y) = (1 + coth(x) * cot(y)) / (cot(x) + cot(y)) sinh(2*x) = 2*sinh(x)*cosh(x) cosh(2*x) = cosh(x)^2 + sinh(x)^2 tanh(2*x) = 2*tanh(x)/(1 + tanh(x)^2) sinh(x/2) = +-sqrt((cosh(x) - 1)/2) (符号は x>0 で +、x<0 で -) cosh(x/2) = sqrt((cosh(x) + 1)/2) sinh(x) + sinh(y) = 2*sinh((x+y)/2)*cosh((x-y)/2) sinh(x) - sinh(y) = 2*cosh((x+y)/2)*sinh((x-y)/2) cosh(x) + cosh(y) = 2*cosh((x+y)/2)*cosh((x-y)/2) cosh(x) - cosh(y) = 2*sinh((x+y)/2)*sinh((x-y)/2) sinh(x)*sinh(y) = (cosh(x+y) - cosh(x-y))/2 cosh(x)*cosh(y) = (cosh(x+y) + cosh(x-y))/2 sinh(x)*cosh(y) = (sinh(x+y) + sinh(x-y))/2 asinh(x) = log(x + sqrt(x^2 + 1)) acosh(x) = log(x + sqrt(x^2 - 1)) atanh(x) = log((1 + x)/(1 - x))/2 acoth(x) = log((x + 1)/(x - 1))/2 sin(j*x) = j*sinh(x) cos(j*x) = cosh(x) tan(j*x) = j*tanh(x) sinh(j*x) = j*sin(x) cosh(j*x) = cos(x) tanh(j*x) = j*tan(x) ここに j = sqrt(-1) sinh(x + 2*k*π*j) = sinh(x) cosh(x + 2*k*π*j) = cosh(x) tanh(x + k*π*j) = tanh(x) ここに k = 0, 1, 2, 3, .. asin(j*x) = j*asinh(x) acos(j*x) = +-j*acosh(x) atan(j*x) = -j*atanh(x) asinh(j*x) = j*asin(x) acosh(j*x) = +-j*acos(x) atanh(j*x) = j*atan(x)
以上、古典的な伝送線路理論の基本を概説しましたが、 2導体系の伝送路で直面する問題についてはこれで十分間に合います。
2本の平行導体や1本の導体と大地による電気通信は極めて古い時代に開発された 技術ですから、一様な線路に関する研究も 1855 年のW.Thomson(Load Kelvin) 時代からの歴史があり、解説書も数多いのですが、その重要性から未だに研究も続 けられているという息の長い分野で、 最後に、この問題の重要な応用について、 簡単に触れて終りにしたいと思います。
漏話(cross talk)や多相送電路等で問題になる多導体系の場合は、 (1.6), (1.8) 等の、V, I を各導体の電圧、電流を要素としたベクトルに拡張し、 (R + j*ω*L) をインピーダンス・マトリクス、 (G + j*ω*C) をアドミタンス・マトリクスに拡張することで、 2導体系と平行した素直な取扱ができます。
この場合は、 インピーダンス・マトリクスには相互インダクタンス、 アドミタンス・マトリクスには相互キャパシタンスが含まれますから、 時間領域で考えるにしても、周波数領域で考えるにしても、 相互結合を含む、回路の連立微分方程式を扱うことになって、 かなり複雑になりますが、 固有値問題として扱うことで、 インピーダンス・マトリクスとアドミタンス・マトリクスが対角化できて、 相互干渉のない独立した2導体系の集合に変換できるため、 取扱が極めて簡単になります。
最近は、この分野の著作も多く、例えば、
J.A.Brandao Faria,- Multiconductor Transmission-Line Structures (John Wiley & Sons, Inc.) 1993, ISBN 0-472-57443-0等をご覧ください。
Transmission-Line Modeling Methodと呼ばれる、 偏微分方程式の新しい数値計算技法としての応用は、ごく最近の話題です。 (注 7)
例えば、損失が無視できる同軸ケーブルの場合は極座標(r-θ)表示で解いた Maxwell方程式の解(電界と磁界)を
b
V = ∫Er*dr
a
b 2*π
I = ∫∫r*Hθ*dθ*dr
a 0
ここに
a = 内部導体外径 (m)
b = 外部導体内径 (m)
Er = 電界の半径方向成分 (V/m)
Hθ = 磁界の角度方向成分 (H/m)
と電磁界を電圧/電流に変換すると線路方程式と一致します。
電磁エネルギの伝搬方向と伝搬量は、下記のポインティングベクタ(Poynting's vector) で決まります。 [E*H]はEとHのベクトル積です。
N = [E*H] ここに N = ポインティングベクタ (joul/m^2*s) E = 電界の強さ (V/m) H = 磁界の強さ (ampere-turn/m)
同軸ケーブルの場合は、 Eがケーブルの半径方向、Hは円周方向ですから、 エネルギの流れは軸方向になります。 Nを中心導体から外部導体まで積分すれば、 ケーブルに沿って伝搬する全エネルギが出ますが、 これが V*I に等しいことは、容易に確認できます。
一方、導体に抵抗があれば、 周囲の磁界による導体の軸方向の電位差ができて、 電界の軸方向成分が生まれますが、 この電界と円周方向の磁界から生まれるポインティングベクタは 導体の内部に進む方向で、 このエネルギが導体内部に入り込んで発熱し、 それが導体損失に起因する減衰の起源になります。
減衰の単位は neper/m ですが、これは は2つの電圧ないし電流の比の自然対数で す。工学的には neper を使うのが一番素直なのですが、工事等の現場ではdB が使われることが多く、これは電力比の常用対数の 10 倍ですから、neper との 関係は次のようになります。
dB = 20*log10(exp(Neper)) = 8.686*Neper
例えば、exp(j(ω*t - β*x)) で、時刻 t1、場所 x1 の値が時刻 t1+dt、場所 x1+dx に於ける値に等しいとすると、
ω*(t1 + dt) - β*(x1 + dx) = ω*t - β*xから、
dx/dt = v = ω/β
なお、 宇宙が生まれる以前から存在するという「正弦波」を前提とした「位相速度」 (phase velocity)は、 単一周波数の電磁波の等位相面の伝搬速度ですから、 無歪線路を別にすれば、 物理的実態との直接の関係がなくて、 エネルギの伝搬速度ではありません。 例えば、導波管などで光速を越えることがあります。
エネルギの伝搬速度としては、 複数の周波数成分で運ばれる包絡線の伝搬速度である、 「群速度」(group velocity)、
Vg = (d/dβ)(β*Vp) = Vp + β*(d/dβ)(Vp) ここに Vg = 群速度 (m/s) Vp = 位相速度 (m/s) β = 位相定数 (rad/m)になることのほうが多いのですが、これもまた、 物理的には「異常分散」(anomalous dispersion)と呼ばれる位相特性を持つ、 ごく普通の伝送線路では、光速を越える場合があって、 Sommerfeld と Brillouin が、 群速度が光速を越える場合は、 信号波形の歪みが大きくなって、 信号速度(signal velocity)は光速を越えられないことを明らかにするまでは、 Einstein の特殊相対性理論への攻撃材料として使われたことがありました。 情報やエネルギの伝搬速度の概念は、なかなか微妙な問題が多く、 落し穴や迷路がたくさんあって、今でも研究対象の1つになっています。
なお、無損失線路などで、位相歪みがなければ、位相速度と群速度は一致します。
反射係数の定義から
r = V1*exp(γ*x)/(V1*exp(-γ*x))一方、線路の任意の点から線路を見込んだインピーダンスを Z とすれば、(2.1), (2.2) から Z = V/I に注意して
Z/Z0 = (V1*exp(-γ*x) + V2*exp(γ*x))/(V1*exp(-γ*x) - V2*exp(γ*x))が得られますから、この2式から exp(γ*x) を消去すれば
r = (Z - Z0)/(Z + Z0) (2.8)が得られます。
任意の場所 x に於ける電圧と電流は、線路の電圧と電流の関係
V(x) = V1*exp(-γ*x) + V2*exp(γ*x) I(x) = (1/Z0)*(V1*exp(-γ*x) - V2*exp(γ*x))と、送端を x = 0、受端を x = l とした終端条件
V(0) + I(0)*Zs = Vg V(l) = I(l)*Zrから
V1 = (Zr+Z0)*Z0*exp(γ*l)*Vg /((Z0+Zs)*(Z0+Zr)*exp(γ*l)-(Z0-Zs)*(Z0-Zr)exp(-γ*l)) V2 = (Zr-Z0)*Z0*exp(-γ*l)*Vg /((Z0+Zs)*(Z0+Zr)*exp(γ*l)-(Z0-Zs)*(Z0-Zr)exp(-γ*l))が得られるので、x = l とすれば、送端と受端の電圧、電流関係が求まります。
(3.4), (3.5) 式に
Vr = Ir*Zrを追加して、Vr と Ir を消去し
Zin = Vs/Isを計算すれば (4.1) になります。
例えば、下記をご覧ください。
Christos Christopoulos,- The Transmission-Line Modeling Method (Oxford Univ Press, 1995) ISBN019856533X 和訳は C.クリストポロス,- TLM 伝達行列法入門 (培風館) ISBN4-563-03539-4
Smith, P.H.,- Transmission Line Calculator (Electronics, vol. 12, 1939, p. 29-31.)
John Henry Poynting (1852-1914) は Maxwell の教え子の1人で、 University of Birmingham, England の前身となる Mason Science College の 物理学教授ですが、「ポインティングの定理」と呼ばれる、 エネルギの流れを表現する美しい公式は、 その 1884-1885 年の論文によります。
図1で、上側の導体と下側の導体の電流が逆向きになっていることに注意してくださ い。これは直流回路の「往きの電流があれば戻りの電流があるだろう」といったもの ではなくて、TEM 波(Transverse Electric Magnetic wave) と呼ばれ る電磁波の伝搬形態に起因する性質なのです。 TEM 波というのは電場と磁場の両方が横波になっている電磁波で、 導波路が 2 つの導体からなっている場合にしか存在しないのですが、 この種の導波路の典型例が、同軸ケーブル(coaxial cable)とツイン・リード(twin lead)です。
TEM 波の特徴は導波路断面の電場と磁場が静電界/静磁界と同じになることで、 この性質を使うと、線路の一次定数 L と C や、導体面の電荷密度が簡単に計算でき ます。この導体面の電荷の符号は 2 つの導体で反対になっていて、 それが電磁波の進行とともに同じ方向に移動するように見えますから、 電流としては逆方向になるわけです。
注意すべきことは、同じ断面の電流が逆方向でないと TEM 波は伝搬できないこ とで、これが複同軸(bicoaxial)差動伝送路では重要な役割を果たします。
完全な TEM 波は完全導体と無損失誘電体でないと実現できませんが、 実用的な導波路ではこれらの損失の影響が L, C に比べて小さいため、 導波路断面の電場と磁場が静電界/静磁界との一致を前提に計算することができて、 それに損失の影響を R, G として加える手法で十分な精度が得られ、 この伝搬形態をQuasi TEM wave(準 TEM 波)と呼んでいます。
(C)1999/06 平林 浩一