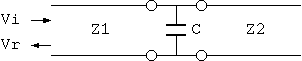
1図 ケーブル(伝送ライン)の接続(コネクタ)部分
高周波ケーブルは長さ方向の電気特性が一様になるように管理されますから、 特性インピーダンスが周期的に変化しない限り(注1)、 ケーブル内部の反射はごく僅かですが、 ケーブルの接続部分でこの一様性を維持するのが難しくて、 かなりの反射が起きることが多く、 この影響をどう評価すればよいかで悩みます。
以下、この接続部分を回路的にどう解釈すればよいかを考えてみますが、 これはケーブル問題だけでなくプリント基板や導波管を含む、 すべての伝送路に共通する原理です。

1図 ケーブル(伝送ライン)の接続(コネクタ)部分
1図のようなケーブル(伝送ライン)始端の接続区間 を考えます。 ここには、コネクタやコネクタとケーブルの接続部分、 プリント基板ならストリップラインと他のパターンの接続部分、ビアホールといった、 線路の一様性が失われる部分の全てを含むことにします。
設計上、 この接続区間の長さは、 伝送される電磁波の波長(注2)に比べて 十分短かくすることが必要不可欠ですから、 実用的な接続区間の電圧と電流は、 その内部でほぼ一様と見倣すことができます(注3)ので、 この接続区間の伝送特性を
Z0 = 接続区間の平均特性インピーダンス (Ohm)
γ = 接続区間の平均伝搬定数
= α + j*β
α = 接続区間の平均減衰定数 (neper/m)
β = 接続区間の平均位相定数 (rad/m)
l = 接続区間の長さ (m)
j = sqrt(-1)
を持つ伝送線路と解釈すると、2図のようになります。
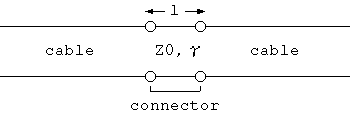
2図 ケーブル(伝送ライン)の接続区間の回路モデル
まず、TDR 測定等で問題になる「反射波」に対する影響から考えることにしますが、 反射波は反射点の入力インピーダンスで決まりますから、 接続区間の影響を接続区間始端の入力インピーダンスから評価してみましょう。
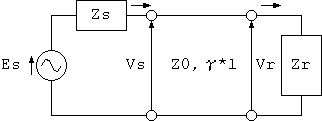
接続区間の後ろのケーブル以降の全回路を ケーブルの入力インピーダンス Zt (Ohm) として 1つのインピーダンス素子にまとめることにすれば、 3図のように解釈することができます。
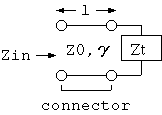
3図 ケーブル(伝送ライン)の接続区間の回路モデル
3図の回路の入力インピーダンス Zin は、 伝送線路の良く知られた関係式、
Zin/Z0 = (Zt/Z0+tanh((α+j*β)*l))/(1+(Zt/Z0)*tanh((α+j*β)*l)) (1)で表現できます。
このケースのように、 接続部分が短く、損失が小さい場合は、 β*l<<1 かつα*l<<1 が成り立ちますから、
tanh((α+j*β)*l)) 〜 α*l+j*β*lになって(注4)、(1) 式は次ぎのように近似できます。
Zin/Z0 = (Zt/Z0+α*l+j*β*l)/(1+(Zt/Z0)*(α*l+j*β*l)) (2)
この接続部分の回路的解釈の最も簡単な可能性としては、 4図の直列等価回路
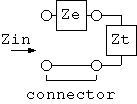
4図 直列等価回路
か、 5図の並列等価回路
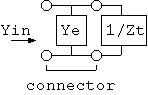
5図 並列等価回路
になりますが、 まず、直列等価回路から考えます。
この場合は、
Zin = Ze + Ztですから、
Ze = Zin - Zt
= (Z0^2-Zt^2)((α*l)*(Z0+Zt*α*l)+Zt*(β*l)^2
+ j*β*l*Z0)/((Z0+Zt*α*l)^2+(Zt*β*l)^2)
になりますが、α*l<<1, β*l<<1 の条件を活かして、下記のように近似できます。
Ze = Zin - Zt
= (Z0^2-Zt^2)(Z0*α*l + j*β*l*Z0)/Z0^2 (3)
ここで、位相定数に関する下記の基本的な関係
β = ω*/v ここに ω = 角速度 (rad/s) = 2*π*f f = 周波数 (Hz) π = 3.14159265.. v = 電磁波の位相速度 (m/s)を考慮すれば、(3) 式は
Ze = (Z0^2-Zt^2)(α*l + j*ω*l/v)/Z0となって、
Ze = Re + j*ω*Le ここに Re = Zt*(Z0/Zt - Zt/Z0)*α*l (Ohm) (4) Le = Zt*(Z0/Zt - Zt/Z0)*l/v (H) (5)接続部分を 抵抗 Re とインダクタンス Le の直列回路として理解することができる ことになります。
ここで、 l/v は電磁波が接続部分を通り抜ける時間 であることに注意してください。 つまり、電磁波の伝搬遅延がインダクタンスとして解釈されることになります。 また、減衰が抵抗として解釈されることは当然です。
接続区間のインピーダンス・マッチングが取れていて、 Z0 = Zt の場合はリアクタンス分がなく、 これが「無反射」の意味です。
Z0 < Zt の場合は負のインダクタンスになりますが、 この場合は並列等価回路で考えるほうが自然で、下記のようになります。 (注5)
5図の並列等価回路の場合は、
Yin = Ye + Yt ここに Yt = 1/Ztですから、
Ye = Yin - Yt
= ((Zt^2-Z0^2)*α*l + j*β*l*(Zt^2-Z0^2))/Z0/Zt^2
となって、
Yin = Ge + j*ω*Ce ここに Ge = (Zt/Z0-Z0/Zt)/Zt*α*l (6) Ce = (Zt/Z0-Z0/Zt)/Zt*l/v (7)この場合は、コンダクタンス G とキャパシタンス C の並列回路として理解 することができます。
この場合も、l/v は電磁波が接続部分を通り抜ける時間ですから、 電磁波の伝搬遅延がキャパシタンスとして解釈され、 減衰がコンダクタンス(抵抗)として解釈されることになります。 抵抗は熱損失を生み、 インダクタンスやキャパシタンスのエネルギ蓄積機能は遅延を生み出します。
以上をまとめると、線路の接続部分として、 次ぎのような等価回路が得られます。 通常の接続区間の損失は他の部分に比べて十分小さいですから、 Re や Ge は無視できるのが普通です。
| 条件 | 等価回路 | パラメータ |
|---|---|---|
| Zt<Z0 | 
| Le = (Z0/Zt-Zt/Z0)*Zt*l/v Re = (Z0/Zt-Zt/Z0)*Zt*α*l |
| Zt>Z0 | 
| Ce = (Zt/Z0-Z0/Zt)/Zt*l/v Ge = (Zt/Z0-Z0/Zt)/Zt*α*l |
ここに Zt = 接続部分の後に接続される伝送ラインの特性インピーダンス (Ohm) Z0 = 接続部分の平均特性インピーダンス (Ohm) α = 接続部分の平均減衰定数 (neper/m) l = 接続部分の長さ (m) v = 接続部分の電磁波の平均位相速度 (m/s)
波長に比べて十分短い伝送ラインが集中定数素子として理解できるのは当然 ですが、 その性格はその後に接続される伝送ラインによって異なり、 伝送ラインの特性インピーダンスに比べて接続部分の特性インピーダンスが大きければ インダクティブ、 小さければキャパシティブで、 その差が大きい程その値も増加します。
例えば、ケーブルとコネクタの接続点では、 往復2導体の間隔が広くなることが多く、 この場合は、高周波に於ける特性インピーダンスの近似式
Z0 = sqrt(L/C) ここに Z0 = 特性インピーダンス (Ohm) L = インダクタンス (H/m) C = キャパシタンス (F/m)を考えれば、特性インピーダンスの増加になるわけで、 インダクタを挿入したことになりますし、 プリント基板でストリップラインの幅が部分的に広がればキャパシタンス、 狭くなればインダクタンスを接続したのと同じ状態になることが 容易にわかります。
さらに理解を深めるために、 上記の結果をSPICEでシミュレーションしてみましょう。
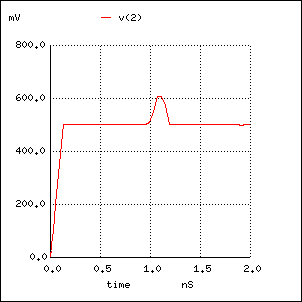
50 Ohm の伝送ラインに約 20 mm の 75 Ohm ラインを挿入したときの TDR (Time Domain Refrectmetry) 波形は次のようになります。
Short 75 Ohm section in 50 Ohm line V1 1 0 PULSE (0 1 0 130P 1) R1 1 2 50 T1 2 0 3 0 Z0=50 TD=0.5N T2 3 0 4 0 Z0=75 TD=0.067N R2 4 0 50 .tran .01p 2n .plot tran v(2)
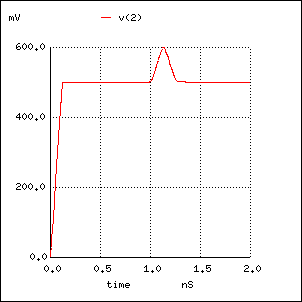
この例では、 接続区間の長さが波長の 2 % になっていますが、 反射波形が台形にならず、山型や谷型になるということは、 この 75 Ohm 区間が伝送波形の高い周波数成分の波長に比べて十分短く、 前記の議論によって、集中定数と見倣せるという意味です。 つまり、この程度の立上り時間なら (注6)、 この 75 Ohm 区間はインダクタンスに見えることになって、 その値は
Le = (75/50 - 50/75) * 0.067e-9 = 2.79e-9 = 2.79 nHになります。
事実、 上記の 75 Ohm ラインをこのインダクタンスで置き換えた結果は下記のようになって、 この解釈の正当性を確認することができます。
Le in 50 Ohm line V1 1 0 PULSE (0 1 0 130P 1) R1 1 2 50 T1 2 0 3 0 Z0=50 TD=0.5N L1 3 4 2.79NH R2 4 0 50 .tran .01p 2n .plot tran v(2)
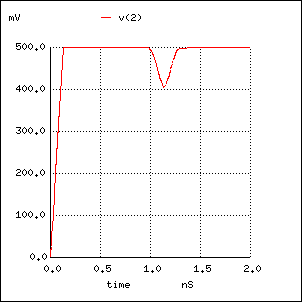
また、上記とは逆に、 75 Ohm ラインの途中に 50 Ohm の短いラインを挿入したときは、 キャパシタンスに見えるはずですが、 これも上記と同様に確認することができます。
まず、分布定数の場合は下記のようになります。
Short 50 Ohm section in 75 Ohm line V1 1 0 PULSE (0 1 0 130P 1) R1 1 2 50 T1 2 0 3 0 Z0=75 TD=0.5N T2 3 0 4 0 Z0=50 TD=0.067N R2 4 0 75 .tran .01p 2n .plot tran v(2)
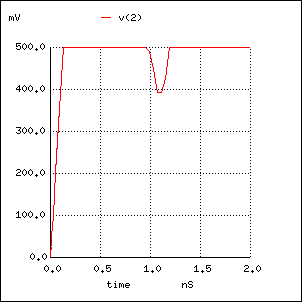
等価キャパシタンスは
Ce = (75 / 50 - 50 / 75) / 75 * 0.067e-9 = 7.44e-13 = 0.744pFですから、これで 50 Ohm ラインを置き換えると、下記のようになって、 TDR 波形の一致を確認することができます。
Ce in 75 Ohm line V1 1 0 PULSE (0 1 0 130P 1) R1 1 2 75 T1 2 0 3 0 Z0=75 TD=0.5N C1 3 0 0.744PF R2 3 0 75 .tran .01p 2n .plot tran v(2)
ネットワーク・アナライザやインピーダンス測定機で 等価回路のパラメータを求めるのはかなり難しいか面倒になるのが普通ですが、 等価インダクタンスと等価キャパシタンスについては、 TDR を使うと比較的簡単で、 以下、その方法を説明します。
6図 インダクタンスを挿入した伝送線路
まず、伝送線路の途中にインダクタンスを挿入した場合、 その電圧反射係数は下記のようになります。 計算は簡単ですから、 必要なら過渡現象論の文献を見てください。
r(t) = r1 + (1 - r1)*exp(-(Z1+Z2)/L*t) ここに r1 = (Z2 - Z1)/(Z2 + Z1)ここでは Z1 = Z2 = Z0 ですから、r1 = 0 になって、
r(t) = exp((-2*Z0)/L*t)今、r(t) を 0 から無限大まで積分すると、
∽ ∫r(t)*dt = L/2/Z0 0つまり、
L = 2*Z0*∫r(t)*dt (8)を実測すれば L が決まります。
7図 キャパシタンスを挿入した伝送線路
同様に、キャパシタンスを挿入した場合は、
r(t) = -r1 + (1 + r1)*exp(-(1/Z1 + 1/Z2)/C*t) ここに r1 = (Z2 - Z1)/(Z2 + Z1)ですから、先程と同じように r(t) を 0 から無限大まで積分して、
C = 2/Z0*∫r(t)*dt (9)の関係が得られます。
(6), (7) の積分は、 測定された波形をコンピュータで処理すれば簡単ですが、 人手で手っ取り早くやるのでしたら、反射波形の高さの平均と幅の平均を読みとって、 波形の山、谷を同じ面積の長方形に変換し、 下記のように計算する程度でも、実用上十分な精度が得られます。
L = 2*a*w*Z0 (反射波が上に出る場合) C = 2*a*w/Z0 (反射波が下に出る場合) ここに a = 反射波形の平均高さ (反射係数) w = 反射波形の平均幅 (s) Z0 = 線路の特性インピーダンス (Ohm)
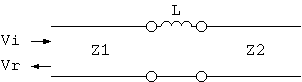
以上、接続部分が反射波に与える影響を考えてきましたが、 次に、進行波に与える影響を考えます。
7図 伝送回路
進行波に影響を与えるのは伝送特性ですから、 7図の伝送回路の良く知られた関係、
Vr = Vs*cosh(γ*l) - Z0*Is*cosh(γ*l) (10) Ir = -Vs/Z0*cosh(γ*l) + Is*cosh(γ*l) (11) ここに γ = 伝搬定数 = α + j*β α = 減衰定数 (neper/m) β = 位相定数 (rad/m) l = 線路の長さ (m) Vs = 線路送端の電圧 (V) Is = 線路送端の電流 (A) Vr = 線路受端の電圧 (V) Ir = 線路受端の電流 (A)から出発します。
Vr = Ir*Zr (12) Vs = Es - Is*Zs (13) ここに Zr = 受端に接続された負荷インピーダンス (Ohm) Zs = 信号源の内部インピーダンス (Ohm) Es = 信号源の電圧 (V)ですから、(8)(9)(10)(11) から Is, Ir, Vs を消去すれば、下記のようになります。
Vr/Es = Zr/((Zs+Zr)*cosh(γ*l) + (Zs/Z0+Zo/Zr)*Zr*sinh(γ*l)) (14)伝送線路を伝搬する電磁波の波長に比べて、伝送線路の長さが十分短く、 かつ、損失が十分小さければ、γ*l<<1 が成り立ちますから、
cosh(γ*l) 〜 1 sinh(γ*l) 〜 γ*lと近似できて、
Vr/Es 〜 Zr/(Zs + Zl + (Zs/Z0+Z0/Zr)*Zr*γ*l)) (15)になります。
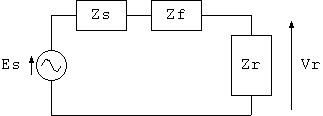
8図 l が小さいときの、7図の直列等価回路
ここで、8図の直列等価回路に於ける Vr/Es = Zr/(Zs + Ze + Zr) を (15) 式と比べれば、
Zf = Rf + j*ω*Lf として、 Rf = Zr*(Zs/Z0 + Zs/Zr)*α*l (16) Lf = Zr*(Zs/Z0 + Zs/Zr)*Z0*l/v (17)となって、透過波に対しては接続部分がインダクタンスとして機能する ことになります。 (注7)
ここで、6図のケースを考えると、 インダクタを通り抜ける電磁波の電圧透過係数 t(t) は次のようになります。
t(t) = (1 + r1)*(1 - exp(-(Z1+Z2)/L*t)) ここに r1 = (Z2 - Z1)/(Z2 + Z1)つまり、 接続点のインピーダンスミスマッチは透過波形を指数的に鈍らせる ことになって、 Z1 = Z2 = Z0 の場合、その時定数は Lf/Z0/2 になります。
反射波形の立上りは Le, Ce に関係なく極めて速いのですが、 透過波形の立上りは Lf が大きい程遅くなることに注意してください。
上記の結果も、SPICEでシミュレートしてみるとよく理解できると思います。
まず、50 Ohm の伝送ラインに平均特性インピーダンス 200 Ohm、 電磁波の通過時間 0.01nS の接続部分を入れたとき、 接続部分を透過した波形は次ぎのようになります。
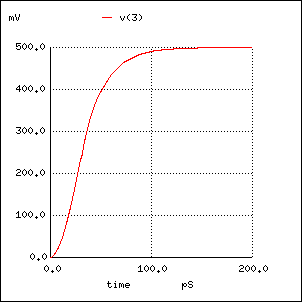
Incident wave after 200 Ohm short section in 50 Ohm line V1 1 0 PULSE (0 1 0 30P 1) R1 1 2 50 T1 2 0 3 0 Z0=200 TD=0.01N R2 3 0 50 .tran .1p 200p .plot v(3)
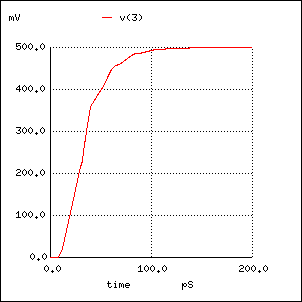
ここで、パルスの立上り時間 (30pS) をもっと短くすると、 透過波形の立上りが遅くなる理由が多重反射によるものであることがよくわかります。
透過波形に対する等価インダクタンス Lf は
Lf = 200*(1 + 50*50/200^2)*0.01e-9 = 2.125e-9 (H)ですから、200 Ohm の伝送ラインを 2.125nH のインダクタンスで置き換えると、 次ぎのようになります。
Incident wave after inductance of 2.12nH in 50 Ohm line V1 1 0 PULSE (0 1 0 30P 1) R1 1 2 50 L1 2 3 2.12N R2 3 0 50 .tran .1p 200p .plot v(3)
Lf を実測する場合は、反射波と同じように、 透過波について、(6) 式を使うこともできますが、 (5), (7), (17) から、下記の関係が得られますので、 TDR の結果から求めることもできます。
Lf = (Z0^2+Zt^2)/(Z0^2-Zt^2)*Le (Zt > Z0 のとき)
= (Zt^2+Z0^2)/(Zt^2-Z0^2)*Le (Zt < Z0 のとき)
以上で、 伝送線路の接続点、あるいは、不均一部分を集中定数回路として解釈すると、 極めて見通しがよくなって、 反射波については、 不連続部分の平均特性インピーダンスが回路の特性インピーダンスより大きければ インダクタンス、 小さい場合はキャパシタンスに見え、 透過波については、 いずれの場合もインダクタンスに見えるということが理解できると思います。
不連続部分が透過波の立上りを遅くするという点は、 よく見落とされていますので、注意が必要です。
ケーブルの長さ方向の特性インピーダンスの変化がわずかでも、 その変化に周期性がある場合は、 その周期が 1/4 波長の奇数倍になる周波数で、 全ての反射波が同位相で加算されますから、 予期しない大きな減衰を生みます。
パルス波形の場合は、 その波形に大きな影響を与えるスペクトル成分の上限の波長との比較になります。 よく使われる目安としては、
Fmax = 0.35/Tr ここに Tr = パルスの立上り時間 (S) Fmax = 波形に影響を与えるスペクトルの最高周波数 (Hz)があって、これを受け入れることにすれば、
λ = 8.57e8 * Vr * Tr (a) ここに λ = 波長 (m) Vr = 速度係数 (電磁波の伝搬速度 / 真空中の光速)となります。
8.3. 接続部分内で電圧電流がほぼ一様と見倣せるかどうかの判断
接続部分を集中定数と見倣せるかどうかは、 TDR 波形で考えると極めて明解になります。 例えば、「SPICEによるシミュレーション」の例で、 立上がり時間をもっと短くして、 得られた波形を観察してみてください。 波形が台形になってくれば、 接続部分先端の反射と後端の反射が完全に分離できているわけですから、 集中定数回路と見倣すのは無理で、 分布定数回路として理解しなければなりません。
接続部分先端の反射と後端の反射が混じり合った状態が、 「点」として理解できるための条件です。
8.4. tanh((α+j*β)*l)) 〜 α*l+j*β*l
よけいなお世話かもしれませんが、
tanh((α+j*β)*l)) = (tanh(α*l)+tanh(j*β*l))/(1+tanh(α*l)*tanh(j*β*l)) = (tanh(α*l)+j*tan(β*l))/(1+tanh(α*l)*jtan(β*l))ですが、α*l<<1 なら
tanh(α*l) 〜 α*lまた、β*l<<1 なら、
tan(β*l) 〜 β*lですから、
tanh((α+j*β)*l)) 〜 α*l + j*β*l
4図で Ze = j*ω*L、5図で Ye = j*ω*C として、 Zin と Yin が等しくなる条件を考えれば、
C = -L / (Z^2 + j*ω*L*Z)ですから、ω*L<<Z なら、
C = -L / Z^2になりますが、 この関係は、(8) と (9) からも(積分の符号を考慮して)得られます。
0.5nS (TD=0.5N) の遅延は、速度係数 1.0 として、 0.15 m の長さになります。 一方、130pS (130P) の立上り時間を (a) の評価すれば、 波長を 0.11 m と見倣すことになり、 このシミュレーションの結果から見る限り、 (a) 式で評価される長さ程度までなら、 集中定数と見倣しても大きな誤差は生まれないことがわかります。
透過波に対する等価回路としては、7図の等価回路を使うこともできて、 この場合は、
Cf = (1/Zs + 1/Zr)*z0*l/vになります。 解釈としてはこのほうが素直ですが、実務上は1つで間に合わせるほうが楽ですし、 同じ結果になることが直観的にわかりますので、直列等価回路だけにしました。
なお、下記の関係があることに注意してください。
zs*zr = Lf/Cfつまり、Lf, Cf は平均インピーダンスと深い関係があります。
(C)2001 平林 浩一