非線形回帰分析 (non-linear regression analysis)

誤差を含むデータに線形モデルをあてはめる場合は線形回帰分析 (linear regression) を使いますが、非直線モデルをあてはめる場合は少し難しくなって、 Levenberg-Marquardt 法などの工夫が必要になります。

以前なら自分でプログラムを書くわけですが、今はgnuplotにこの機能も組み込まれましたので、当社でよく必要になる、高周波の減衰特性を求める例をもとに、 非線形回帰分析 (non-linear regression analysis) の具体的な使いかたを説明します。

1. ケーブルの高周波に於ける減衰特性

一般に、高周波に於けるケーブルの減衰特性は次式で表現できます。

  α = a * sqrt(f) + b * f                           (1)
  ここに、
	α = 減衰定数 (neper/m)
	f = 周波数 (Hz)
	a = 導体損失で決まる定数
	b = 誘電体損失で決まる定数

導体損失としては表皮効果(skin effeect)によるものが最大で、次いで近接効果(Proxmity effect)、シールドや近接導体に於ける渦電流損失が続きます。これらすべての渦電流損失には導体に於ける電磁波の侵入の深さが関係しますから、周波数の平方根に比例して実効導体断面積が減り、交流抵抗も周波数の平方根に比例して増加することになります。

誘電体損失としては絶縁体の誘電体損失が最大で、次いでジャケットや近接誘電体内部の誘電体損失が続きます。誘電体損失は電磁場中の誘電体を構成する分子の振動によるものですから、

  G = ω * C * D                                      (2)
  ここに、
	G = ケーブルのコンダクタンス (S/m)
	G = ケーブルのコンダクタンス (S/m)
	ω = 角周波数 (rad/s)
	   = 2 * π * f
	C = ケーブルのキャパシタンス (F/m)
	D = tan(δ)
	  = 誘電体損率

の関係があって、長さが無視できないケーブルの基本的な特性

  α = R / (2 * Z0) + G * Z0 / 2                      (3)
   ここに、
	R = ケーブルの(高周波)電気抵抗 (Ω/m)
	Z0 = ケーブルの特性インピーダンス (Ω)

を考慮すれば、下記の関係が得られます。

  D = b / (π * C * Z0)                            (4)

すなわち、高周波での測定が難しい D が減衰特性から求められることになります。もちろん、これは D が周波数に関係なく一定な場合で、 D に周波数特性がないときの話ですが、 D の周波数特性が無視できるかどうかは、 log(α) と log(f) の関係が直線かどうかで確認でき、通常のケーブルなら、まず (1) 式が成立します。

2. 非線形モデルのあてはめ

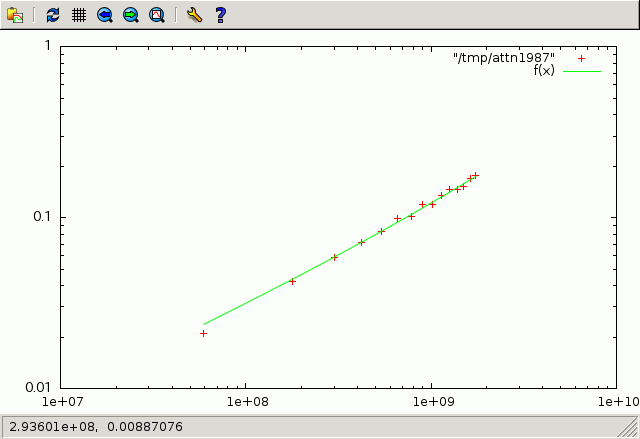
以下、gnuplotを使って、高周波ケーブルの減衰特性の実測値に (1) 式をあてはめて、定数 a, b を求める実例を解説します。

実測値には中西さんが共振法で求めた 3200 の減衰定数を使いました。

#! /bin/sh
TMP="/tmp/attn$$"
trap 'rm -f $TMP fit.log; exit 0' 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
echo "\
# 3200 attenuation
# freq. alphe (neper/m)
  59.28e6 0.0210
 178.93e6 0.0421
 299.28e6 0.0583
 419.20e6 0.0719
 539.86e6 0.0831
 660.22e6 0.0985
 780.63e6 0.1009
 901.49e6 0.1189
1021.05e6 0.1195
1143.23e6 0.1338
1261.17e6 0.1461
1384.71e6 0.1461
1501.65e6 0.1509
1624.86e6 0.1697
1744.92e6 0.1754" >$TMP
{
echo "\
set logscale x
set logscale y
f(x)=a*sqrt(x)+b*x
fit f(x) \"$TMP\" via a,b
plot \"$TMP\", f(x)
pause -1 'Press any ley to exit. > '"
read x
} | gnuplot
exit 0

この scriot を実行すると、下記の結果が得られます。

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 2.83712e-06      +/- 1.61e-07     (5.675%)
b               = 3.197e-11        +/- 4.645e-12    (14.53%)


correlation matrix of the fit parameters:

               a      b      
a               1.000 
b              -0.980  1.000

gnuplotはよくできた作図プログラムですが、設計がUnix的でなく、自動化のためのバッチ処理を考えていませんので、データを一時ファイルに書き込んでから、コマンドをパイプラインで入力し、最後に終了タイミングをオペレータが指示できるようにしています。

学習用 script を簡単にするため、グラフ表示は必要最小限の機能にしていますが、 gnuplotには多彩な機能がありますので、ドキュメントを見ながら少しづつ覚えていってください。

3. D の測定

(4) 式の D は絶縁体の高周波特性を決める重要なパラメータで、絶縁体に含まれる分子の種類と含有量で決まりますが、通常使用する絶縁物の値を実測しておくと、新しく設計するケーブルの高周波減衰を高い精度で予測することができます。

kh@mogami-wire.co.jp, 2015-11-13