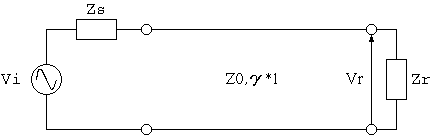
ケーブル伝送波形の減衰と歪みは有限個の L, R, G, C から構成される一般の電子回路とはかなり違います。 (注1)
ここでは、Fourier変換による周波数領域でケーブル伝送波形を求めるための、 ケーブル周波数特性モデルの作成と、その使いかたを解説します。
まず、ケーブルの伝送特性を表すシステム関数を求めます。 (注2)
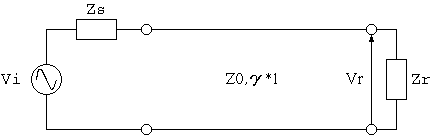
ここに、 Vi = ケーブル送端の(信号)電圧源 Zs = 信号源の内部インピーダンス (Ω) Z0 = ケーブルの特性インピーダンス (Ω) γ = ケーブルの伝搬特性 = α + j*β α = ケーブルの減衰定数 (neper/m) β = ケーブルの位相定数 (rad/m) j = sqrt(-1) l = ケーブルの長さ (m) Zr = ケーブル受端の負荷インピーダンス (Ω) Vr = ケーブル受端の電圧 (V)
1図 ケーブル伝送
1図の回路で、信号電圧に対する受信電圧の比は下記のようになります。 (注3)
Vr/Vi = Zr/(Zs+Zr)/(cosh(γ*l)+Z0/(Zs+zr)(1+Zs*Zr/Z0^2)*sinh(γ*l)) (1)
1図でケーブルを除いて、信号源と負荷を直結した場合は、
Vr/Vi = Vi*Zr/(Zs+Zr) (2)ですから、ケーブルのシステム関数は
H(f) = 1/(cosh(γ*l)+Z0/(Zs+zr)(1+Zs*Zr/Z0^2)*sinh(γ*l)) (3)です。
これは、(3) のシステム関数に入力信号 Vi を入れると出力信号 Vr が得られることを意味します。
つまり、任意の入力信号 f(t) について、 下記の手順で出力信号 g(t) が得られることになります。
ケーブルの伝搬特性は特性インピーダンスと伝搬定数で決まりますが、 高周波なら下記のモデルで表現できます。 周波数が低くなると、もっと複雑になりますが、 伝送波形を求める場合はこの近似で十分間に合います。
Z0 = 特性インピーダンス (Ω)
= sqrt(L/C)
L = 高周波に於けるケーブルのインダクダンス (H/m)
C = 高周波に於けるケーブルのきゃぱしたんす (F/m)
α = 減衰定数 (neper/m)
= Rdc + sqrt(f*Rdc)/(4*Z0)
Rdc = 直流抵抗 (Ω/m)
β = 位相定数 (rad/s)
= c*Vr + α
= 1/sqrt(L*C) + α
c = 真空中の光速 (2.99792458e8)
Vr = ケーブルの速度係数 (0 < Vr <= 1)
特性インピーダンスはケーブルを伝搬する電磁波の 磁界成分に対する電界成分の比ですから、 特性インピーダンスが大きくなると、 ケーブルの導体に流れる電流が減って、 導体中のジュール熱による損失が減り、 減衰が減ることになります。
α と β のいずれも周波数の平方根に比例する成分が出て来ますが、 これがケーブル独特の歪の原因になります。 (注4)
PE (Polyethylenie) のような高周波特性の良い絶縁材料を使っていれば、 誘電体損失は導体損失に比べて十分低いので無視できますが、 誘電体損失による減衰は
G = ω * C * tan(δ) ここに、 G = 誘電体損失による減衰 (G*m) ω = 角周波数 (rad/s) = 2 * π * f π = 3.1415.. f = 周波数 (Hz) C = ケーブルのキャパシタンス (F/m) tan(δ) = 誘電体の誘電正接ですから、減衰定数は下記のようになります。
α = 減衰定数 (neper/m)
= Rdc + sqrt(f*Rdc)/(4*Z0) + ω*C*tan(D)/2/Z0
ケーブルの周波数領域モデルがわかれば、 前記の手順で任意の入力信号に対する出力波形を計算できますが、 以下、理解しやすいように、簡単で実用的な事例をつけておきます。 手軽に実験できるように、c や c++ でなく、awk script で書いてありますが、 複素数の計算が多い場合は c++ を使うほうが楽です。
まず、通常の伝送線路では送受端のインピーダンスマッチングが取れていますから
Zs = Zr = Z0が成り立ち、この場合 (3) 式は下記のように簡略化できます。
H(f) = exp(-γ*l) (4)
= exp(-α*l)*exp(-j*β*l)
= exp(-α*l)*(cos(β*l)-j*sin(β*l))
数値計算の場合は無限時間の積分ができず、 FFT(Fast Fourier Transform)を使うのが普通で、 入力波形は周期関数に限定されますが、 ここではパルス波形の代表である方形波を考えると、 下記のように計算することができます。 (注5)
#! /bin/sh
M=9 # 2^M = 1 周期のサンプル数
len=100 # ケーブル長 (m)
Z0=110 # 特性インピーダンス (Ohm)
a0=0.201 # 直流抵抗 (Ohm/m)
a1=3.96e-6 # 高周波の減衰定数(neper/m)/sqrt(f) .. f = 周波数(Hz)
/usr/bin/awk '
BEGIN {
M = '$M'
z0 = '$Z0' # Z0
a0 = '$a0' # Rdc
a1 = '$a1' # alpha/sqrt(f)
pulse(20e-9, 20e-9, 142e-9, 326e-9, M)
exit 0
}
# パルス波形生成
# tr = 立上り時間 (s)
# tf = 立下がり時間 (s)
# pw = パルス幅 (s)
# per = 周期 (s)
# 2^M = 1 周期のサンプル数
function pulse(tr, tf, pw, per, M, i, N, N1, N2, N3, v) {
N = 2^M
N1 = int(N * tr / per + 0.5)
N2 = int(N * (tr + pw) / per + 0.5)
N3 = int(N * tf / per + 0.5) + N2
for (i = 0; i < N; i++) {
t = per * i / N
if (i < N1)
v = i / N1
else if (i <= N2)
v = 1
else if (i < N3)
v = (i - N3) / (N2 - N3)
else
v = 0
print t, v
}
}
' | /usr/local/bin/fft | /usr/bin/awk '
BEGIN {
M = '$M'
z0 = '$Z0' # Z0
a0 = '$a0' # Rdc
a1 = '$a1' # alpha/sqrt(f)
len = '$len'
}
{
# F(f)
f = $1 # 周波数
x = $2 # F(f) の実部
y = $3 # F(f) の虚部
# ケーブルの周波数モデル
b = a1 * sqrt(f) * len
if (i == 0)
a = b
else
a = b + a2 * f^a3 * len
if (NR == 0) # DC
a = z0 / (z0 + a0)
else
a = exp(-a)
# F(f)*H(f)
u = a * cos(b)
v = -a * sin(b)
w = x
x = w * u - y * v
y = w * v + y * u
print f, x, y
}' | fft -i
exit 0
この sf script で使っているfftpというコマンドは フーリエ変換と線形システムの基礎 (2) - 例題 で解説したものです。
Fourier変換については フーリエ変換と線形システムの基礎 (1) - 解説 を見てください。
この script を実行したときの ケーブル入力波形と ケーブル出力波形を付けておきます。
有限個の L, C, R, G から構成される、 一般の電子回路のステップ応答は指数関数的波形になりますが、 これは回路の方程式が常微分方程式になるためです。
一方、無限個の L, C, R, G から構成され、 回路の方程式が偏微分方程式になる伝送線路の場合は、 ステップ応答が誤差関数的波形になって、 収束が遅いため、 電子回路でお馴染みの立上り時間の定義が使えないとか、 かなり様相が異なって、 SPICEなどの回路シミュレータで解析する場合も、 工夫が要ります。
線形システムのインパルス応答 h(t) のFourier変換をシステム関数と呼びます。
∽
H(ω) = ∫h(t)*dt = exp(-α(ω)) * exp(-β(ω))
-∽
ここに、
H(ω) = システム関数
h(t) = インパルス応答
α(ω) = 減衰量 (neoer)
β(ω) = 位相遅れ (rad)
ω = 角周波数 (rad/s)
線形システムの入力波形 f(t) と出力波形 g(t) のFourier変換をそれぞれ F(ω), G(ω) とすると
G(ω) = F(ω) * H(ω)が証明できて、
∽
g(t) = 1/(2π)*∫ F(ω)*H(ω)*exp(j*ω*t)*dω
-∽
Fourier逆変換により出力波形が得られます。
伝送線路理論の基礎を見てください。
伝送線路の SPICE モデルを見てください。
インピーダンスマッチングがとれていない場は H(f) に (4) 式でなく (3)
式を使います。
注4 - ケーブル伝送の2次定数の近似式