一様な伝送線路の途中にコネクタなどの接続部分があると、 線路の一様性が失われ、 その部分が集中回路としてのインダクタンスやキャパシタンスに見えることは ケーブル接続部分の回路モデルで解説しましたが、 この等価インダクタンスや等価キャパシタンス を実測しなければならないことも多く、 この場合はTDR(Time Domain Reflectometry)を使うのが簡単です。
この方法についてはたくさんの解説(注1)がありますが、 根拠をきちんと説明した資料がないようですから、 以下、その考え方を説明しておきます。 基本的には電気工学の過渡現象問題になります。
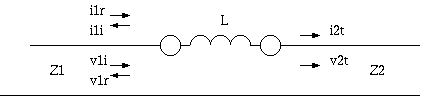
1図のように 特性インピーダンス Z1 の線路と特性インピーダンス Z2 の線路の接続点に 直列インダクタンス L が挿入された回路を考えます。

1図 直列インダクタンス
伝送線路ですから電圧、電流を進行波、反射波、 透過波に分解して、 それぞれ別々に考えるというHeavisideのアイデアが必要ですが、 それ以外は集中定数の電気回路と同じです。
v1i + v1r = v2t + L*(d/dt)(i2t) i1i + i1r = i2t v1i = i1i * Z1 v1r = i1r * Z1 v2t = i2t * Z2 ここに、 v1i = 入射波の電圧 (V) v1r = 反射波の電圧 (V) i1i = 入射波の電流 (A) i1r = 反射波の電流 (A) v2t = 透過波の電圧 (V) i2t = 透過波の電流 (A) Z1 = 入射側線路の特性インピーダンス (Ω) Z2 = 透過側線路の特性インピーダンス (Ω) L = 特性インピーダンス Z1 と Z2 の線路の間に挿入されたインダクタンス (H)求めなければならない波形は V1r ですが、 時間的に不連続ですから、まず飛躍のない(連続な) i2t を求めます。 Z1 の線路にTDRのステップ電圧 V が到達した時間を t = 0 とすれば、
L * (d/dt)(i2t) = (Z1 + Z2) * i2t i2t = 0, i1i = V / Z1 (t = 0) .. 初期条件これは集中定数回路の R-L 直列回路に直流起電力を加える場合とまったく同じ微分法定式で、
i2t = 2 * Z1 / (Z1 + Z2) * V * (1 - exp(-(Z1 + Z2) / L * t))反射電圧は i1i + i1r = i2t と電圧-電流関係から i1i, i1r, i2t を消去して
v1r = v1i - Z1 / Z2 * v2t
= V - 2 * Z1 / (Z1 + Z2) * V * (1 - exp(-(Z1 + Z2) / L * t))
= V *(Z2 - Z1) / (Z2 + Z1) + 2 * Z2 / (Z2 + Z1) * exp(-(Z1 + Z2) / L * t))
測定器としてのTDRは y 軸を V で規格化した電圧で表示しますから
v1r / V を求めると
v1r / V = (Z2 - Z1) / (Z2 + Z1) + 2 * Z2 / (Z2 + Z1) * exp(-(Z1 + Z2) / L * t)t = 0 で (Z2 - Z1) / (Z2 + Z1) + 2 * Z2 / (Z1 + Z2) に飛躍し、 無限時間経過後に (Z2 - Z1) / (Z2 + Z1) に落ち着きますが、 これは L が存在しないときの値で、 十分な時間がたてば L の影響がなくなることを意味します。
L を求める方法としては v1r / V - (Z2 - Z1) / (Z2 + Z1) の面積を使うのが簡単で
∽
s = ∫(v1r / V - (Z2 - Z1) / (Z2 + Z1)) * dt
0
= 2 * Z2 / (Z2 + Z1)^2 * L
Z1 = Z2 = Z0 つまり、
特性インピーダンス Z0 の一様な線路の途中に L を挿入した場合は
s = L / (2 * Z0)ですから、インダクタンス L の値は
L = 2 * Z0 * s (A) ここに、 s = L 先端の(正規化)反射波から L 後端の(正規化)反射波を引いた部分の面積となります。
念のためこの式の次元解析をしてみると、
左辺(インダクタンス) = M*L^2*T^-2*A^-2 右辺 = Z0 * s = V / I * T = (L^2*M*T^-3*A^-1) / (A) * (T) ここに、 L = 長さの次元 (m) M = 質量の次元 (kg) T = 時間の次元 (s) A = 電流の次元 (A)左辺と右辺の次元は一致します。 これでもある程度納得できますが、 この次元解析を(SI 単位系でなく)Heaviside単位系で実行すると、 TDRの意味が実に明解になります。 (注2)
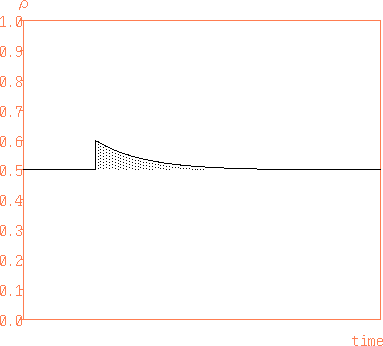
2図 50 Ω伝送線路の途中にインダクタンスを挿入したときのTDR波形
この影を付けた部分の面積から L を求めるのですが、 TDRで使うステップ電圧の立ち上がり時間が 0 ではないため、 測定された面積は真の面積より小さくなりますので、 必要な場合は立ち上がり部分の波形が理論値に近付くように補正します。
なお、 伝送線路の特性インピーダンスと等しいインピーダンスで終端した負荷と 直列に接続されたインダクタンスの値を求める場合も 全く同じであることに注意してください。 終端機器の入力インピーダンスに付随するリード線のインダクタンス を求める場合にも使えます。
3図のように 特性インピーダンス Z1 の線路と特性インピーダンス Z2 の線路の接続点に 並列キャパシタンス C が挿入された回路を考えます。
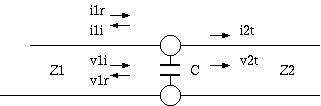
3図 並列キャパシタンス
ケーブル途中の接続点に並列キャパシタンスが出てくることは少ないのですが、 この場合は
v1i + v1r = v2t i1i + i1r = i2t + C * (d/dt)v2t ここに、 C = 特性インピーダンス Z1 と Z2 の線路の接続点に挿入されたキャパシタンス (F)この場合も集中定数の R-C 直列回路と同じ微分方程式になります。
この場合は電流が不連続、電圧が連続ですから、 初期条件 t = 0 で v2t = 0 から v2t を先に求めて
v2t = 2 * Z2 / (Z2 + Z1) * V * (1 - exp(-(1 / (Z// * C) * t))) ここに、 Z// = Z1 * Z2 / (Z1 + Z2) .. Z1 と Z2 の並列接続
反射波は
v1r = -V + 2 * Z2 / (Z2 + Z1) * V * (1 - exp(-(1 / (1 / (Z// * C) * t)))v1r / V を求めると
v1r / V = (Z2 - Z1) / (Z2 + Z1) - 2 * Z2 / (Z2 + Z1) * exp(-(1 / (Z// * C) * t))t = 0 で -1 という短絡状態に飛躍し、 無限時間経過後に (Z2 - Z1) / (Z2 + Z1) に落ち着きますが、 これも C が存在しないときの値で、 十分な時間がたてば C の影響がなくなることを意味します。
C を求める方法としても、(Z2 - Z1) / (Z2 + Z1) - v1r / V の面積を使うのが簡単で
∽
s = -∫(2 * Z2 / (Z2 + Z1) - exp(-1 / (Z// * C) * t)) * dt
0
= -2 * Z1 * Z2^2 / (Z1 + Z2)^2 * C
Z1 = Z2 = Z0 なら
C = -2 * s / Z0 (B)
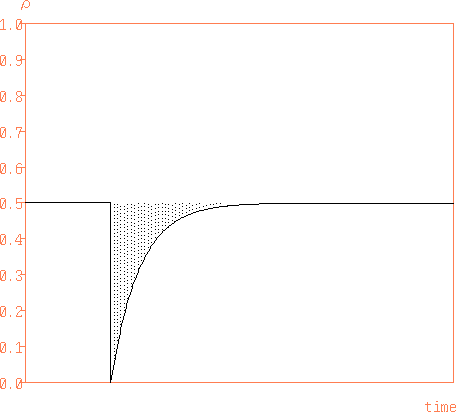
4図 50 Ω伝送線路の途中にキャパシタンスを挿入したときのTDR波形
この影を付けた部分の面積から C を求めるのですが、 現実のTDR測定の場合、ステップ波形の立ち上がり時間がありますから、 負のピーク電圧が 0 にならず、 実際のキャパシタンスより小さな値が得られますので必要なら補正します。
なお、 伝送線路の特性インピーダンスと等しいインピーダンスで終端した負荷と 並列に接続されたキャパシタンスの値を求める場合も 全く同じであることに注意してください。 終端機器の入力インピーダンスに付随する浮遊容量を求める場合にも使えます。
伝送線路の接続部分としては、まず遭遇しませんが、同様の計算で、 線路の途中に直列キャパシタンスが挿入されている場合は
C = -s / 2 / Z0並列インダクタンスが挿入されている場合は
L = s * Z0 / 2が得られます。
インダクタンスとキャパシタンスの両方が存在する場合も同様に解析できますが、 この場合は二次の定数係数線形微分方程式になりますから、 少し複雑になって、条件によっては振動を生じます。
なお、ここでは常識的なTDRを使う方法の根拠を解説しましたが、 周波数特性から寄生回路パラメータを求めることもできます。
4.1. 注1 - TDRによる寄生回路パラメータ抽出の解説
例えば、 Use TDR to measure L and C - Agilent Technologies など、たくさんあります。